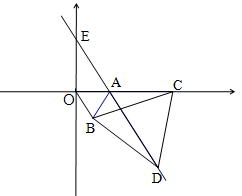
如图,直角坐标系中,点 的坐标为
的坐标为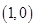 ,以线段
,以线段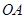 为边在第四象限内作等边
为边在第四象限内作等边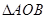 ,点
,点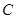 为
为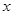 正半轴上一动点
正半轴上一动点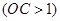 ,连结
,连结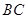 ,以线段
,以线段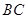 为边在第四象限内作等边
为边在第四象限内作等边 ,直线
,直线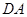 交
交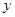 轴于点
轴于点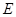 .
.
(1)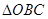 与
与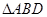 全等吗?判断并证明你的结论;
全等吗?判断并证明你的结论;
(2)将等边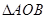 沿
沿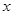 轴翻折,
轴翻折,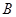 点的对称点为
点的对称点为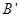 .
.
①点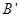 会落在直线
会落在直线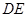 上么?请说明理由;
上么?请说明理由;
②随着点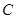 位置的变化,点
位置的变化,点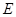 的位置是否会发生变化? 若没有变化,请直接写出点
的位置是否会发生变化? 若没有变化,请直接写出点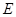 ,若有变化,请说明理由.
,若有变化,请说明理由.
菱形与正方形的形状有差异,我们将菱形与正方形的接近程度记为“接近度”.设菱形相邻的两个内角的度数分别为m°和n°,将菱形与正方形的“接近度”定义为|m-n|.在平面直角坐标系中,抛物线y=x2+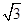 bx+c(b<0)交y轴于点A(与原点O不同),以AO为边作菱形OAPQ.
bx+c(b<0)交y轴于点A(与原点O不同),以AO为边作菱形OAPQ.
(1)当c=-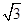 b时,抛物线上是否存在点P,使菱形OAPQ与正方形的“接近度”为0,请说明理由.
b时,抛物线上是否存在点P,使菱形OAPQ与正方形的“接近度”为0,请说明理由.
(2)当c>0时,对于任意的b,抛物线y=x2+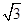 bx+c上是否存在点P,满足菱形OAPQ与正方形的“接近度”为60?若存在,请求出所有满足条件的b与c的关系式;若不存在,请说明理由.
bx+c上是否存在点P,满足菱形OAPQ与正方形的“接近度”为60?若存在,请求出所有满足条件的b与c的关系式;若不存在,请说明理由.
已知反比例函数y= (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y= (x>0)的图象相交于点F(p,q).
(x>0)的图象相交于点F(p,q).
(1)当F点恰好为线段的中点时,求直线AF的解析式(用含a的代数式表示);
(2)若直线AF分别与x轴、y轴交于点M、N,当q=-a2+5a时,令S=S△ANO+S△MFO(其中O是原点),求S的取值范围.
如图,BC是半圆O的直径,点A在半圆O上,点D是AC的中点,点E在 上运动.若AB=2,tan∠ACB=
上运动.若AB=2,tan∠ACB= ,请问:分别以点A、E、D为直角顶点的等腰三角形AED存在吗?请逐一说明理由.
,请问:分别以点A、E、D为直角顶点的等腰三角形AED存在吗?请逐一说明理由.
如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,垂足分别为点E、F.请判断AP与EF的数量关系,并证明你的判断.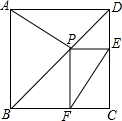
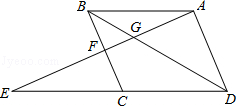
如图,点E为平行四边形ABCD中DC延长线上的一点,且CE=DC.连结AE,分别交BC、BD于点F、G.若BD=6,求DG的长.