已知 、
、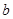 互为相反数,
互为相反数,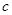 、
、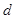 互为倒数,
互为倒数, 的绝对值为2,求
的绝对值为2,求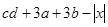 .
.
先化简,再求值: ,其中
,其中 .
.
去括号,并合并同类项:
(1) ;
;
(2) ;
;
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个动点到达终点时,另一个动点也随之停止运动.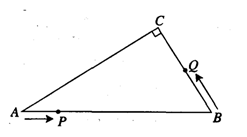
(1)求AC、BC的长;
(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;
(3)当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC是否相似,请说明理由;
(4)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由。
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.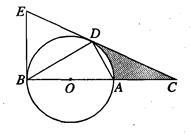
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,∠CBD=30°,则图中阴影部分的面积;
(3)过点B作⊙O的切线交CD的延长线于点E若BC=12,tan∠CDA=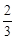 ,求BE的长.
,求BE的长.