如图,在匀强电场中,一电荷量为q=5.0×10-10C的正电荷, 由a 点移到b点和由a点移动到c点,电场力做的功都是3. 0×10-8J,已 知a、b、c三点的连线组成直角三角形,ab=20cm,θ=37°. (sin37°=0.6;cos37°=0.8)
求: (1)a、b两点间的电势差Uab; (2)匀强电场的场强. 
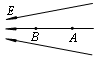
电场中某区域的电场线如图所示,A、B是电场中的两点. 一个电荷量为q = +4.0×10-8 C的点电荷在A点所受电场力FA=2.0×10-4 N,将该点电荷从A点移到B点,电场力做功W = 8.0×10-7J。求:A点电场强度的大小EA;
A、B两点间的电势差U.
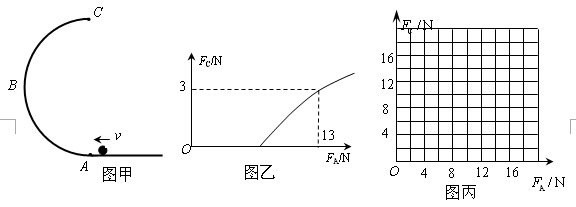
如图甲,ABC为竖直放置的半径为0.1m的半圆形轨道,在轨道的最低点和最高点A、C各安装了一个压力传感器,可测定小球在轨道内侧,通过这两点时对轨道的压力FA和FC.质量为0.1kg的小球,以不同的初速度v冲入ABC轨道.(g取10m/s2)若FC和FA的关系图线如图乙所示,求:当
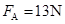 时小球滑经A点时的速度
时小球滑经A点时的速度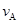 ,以及小球由A滑至C的过程中损失的机械能;
,以及小球由A滑至C的过程中损失的机械能;若轨道ABC光滑,小球均能通过C点.试推导FC随FA变化的关系式,并在图丙中画出其图线.
如图所示,一质量为m、电量为+q、重力不计的带电粒子,从A板的S点由静止开始释放,经A、B加速电场加速后,穿过中间偏转电场,再进入右侧匀强磁场区域.已知AB间的电压为U,MN极板间的电压为2U,MN两板间的距离和板长均为L,磁场垂直纸面向里、磁感应强度为B、有理想边界.求: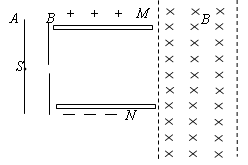
带电粒子离开B板时速度v0的大小;
带电粒子离开偏转电场时速度v的大小与方向;
要使带电粒子最终垂直磁场右边界射出磁场,磁场的宽度d多大?
如图所示,质量为4 kg的物体静止在水平面上,物体与水平面间的动摩擦因数为0.5.物体受到大小为20 N与水平方向成37°角斜向上的拉力F作用时,沿水平面做匀加速运动,求: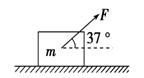
物体加速度的大小.
10 s末的速度和10 s内的位移.(g取10 m/s2,sin37°=0.6,cos37°=0.8)
如图所示,沿水平方向做匀变速直线运动的车厢中,悬挂小球的悬线偏离竖直方向37°角,小球和车厢相对静止,球的质量为1 kg.(g取10 m/s2,sin37°=0.6,cos37°=0.8)
求车厢运动的加速度,并说明车厢的运动情况.
求悬线对球的拉力.