某一空间飞行器从地面起飞时,发动机提供的动力方向与水平方向夹角α=60°,使飞行器恰好沿与水平方向成θ=30°角的直线斜向右上方匀加速飞行,经时间后,将动力的方向沿逆时针旋转60°同时适当调节其大小,使飞行器依然可以沿原方向匀减速飞行,飞行器所受空气阻力不计,求: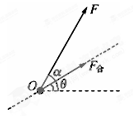
(1)t时刻飞行器的速率;
(2)整个过程中飞行器离地的最大高度.
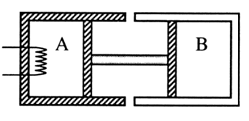
如图,绝热气缸 与导热气缸 均固定于地面,由刚性杆连接的绝热活塞与两气缸间均无摩擦。两气缸内装有处于平衡状态的理想气体,开始时体积均为 、温度均为 。缓慢加热 中气体,停止加热达到稳定后, 中气体压强为原来的1.2倍。设环境温度始终保持不变,求气缸A中气体的体积 和温度 。
甲、乙两车同时同向从同一地点出发,甲车以v1=16 m/s的初速度,a1=-2 m/s2的加速度做匀减速直线运动,乙车以v2=4 m/s的初速度,a2=1 m/s2的加速度做匀加速直线运动,求两车再次相遇前两车相距最大距离和再次相遇时两车运动的时间.
在竖直的井底,将一物块以11 m/s的速度竖直地向上抛出,物块冲过井口时被人接住,在被人接住前1 s内物块的位移是4 m,位移方向向上,不计空气阻力,g取10 m/s2,求:
(1)物块从抛出到被人接住所经历的时间;
(2)此竖直井的深度.
因测试需要,一辆汽车在某雷达测速区沿平直路面从静止开始匀加速一段时间后,又接着做匀减速运动直到最后停止.下表中给出了雷达测出的各个时刻对应的汽车速度数值.求:
(1)汽车在匀加速和匀减速两阶段的加速度a1、a2分别是多少?
(2)汽车在该区域行驶的总位移x是多少?
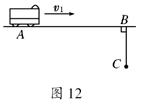
如图12所示,公路上一辆汽车以v1=10 m/s的速度匀速行驶,汽车行至A点时,一人为搭车,从距公路30 m的C处开始以v2=3 m/s的速度正对公路匀速跑去,司机见状途中刹车,汽车做匀减速运动,结果车和人同时到达B点,已知AB=80 m,问:汽车在距A多远处开始刹车,刹车后汽车的加速度有多大?