为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和皮尺,设计如图所示的测量方案,把镜子放在离树(AB)8.7m的点E处,然后观测者沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7m,观测者目高CD=1.6m,则树高AB约是________.(精确到0.1m)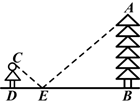
如图,⊙O是正六边形ABCDEF的外接圆,⊙O的半径是2,则正六边形ABCDEF的面积为________.
 |
如图,点C、D在以AB为直径的⊙O上,若∠BDC=28°,则∠ABC=______.
如图,在水平地面上,由A点测得大树BC的顶端C的仰角为60°,A点到大树的距离AB=10m,则大树的高BC为______m.
已知圆锥的底面半径为6,高为8,则它的侧面积是______.
某工厂购买一批直径为40.0mm零件,从中抽样了5件检测其直径,结果如下(单位:mm):40.0,39.8,40.1,40.2,39.9.如果样本的方差大于0.05就要退货,那么该工厂________退货(填“需要”或“不需要”).