如图,两根相互平行的长直导线分别通有方向相反的电流I1和I2,且I1>I2;A、B、C、D为导线某一横截面所在平面内的四点,且A、B、C与两导线共面;B点在两导线之间,B、D的连线与导线所在平面垂直。磁感应强度可能为零的点是( )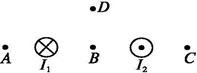
A.A点 B.B点 C.C点 D.D点
如图所示,小球以大小为v0的初速度由A端向右运动,到B端时的速度减小为vB;若以同样大小的初速度由B端向左运动,到A端时的速度减小为vA。已知小球运动过程中始终未离开该粗糙轨道。比较vA、vB的大小,结论是()
| A.vA>vB | B.vA=vB | C.vA<vB | D.无法确定 |
如图所示,质量相等的甲、乙两物体开始时分别位于同一水平线上的A、B两点.当甲物体被水平抛出的同时,乙物体开始自由下落.曲线AC为甲物体的运动轨迹,直线BC为乙物体的运动轨迹,两轨迹相交于C点,空气阻力忽略不计.则两物体()
A.在C点相遇 B.经C点时速率相等 C.在C点时具有的机械能相等
D.在C点时重力的功率相等
如图所示,光滑半球的半径为R,球心为O,固定在水平面上,其上方有一个光滑曲面轨道AB,高度为R/2.轨道底端水平并与半球顶端相切.质量为m的小球由A点静止滑下.小球在水平面上的落点为C(重力加速度为g),则( )
| A.将沿半球表面做一段圆周运动后抛至C点 |
| B.小球将从B点开始做平抛运动到达C点 |
C.OC之间的距离为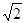 R R |
D.小球从A运动到C的时间等于(1+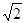 ) ) |
一物体由静止开始从粗糙斜面上的某点加速下滑到另一点,在此过程中重力对物体做的功等于()
| A.物体动能的增加量 |
| B.物体重力势能的减少量与物体克服摩擦力做的功之和 |
| C.物体重力势能的减少量和物体动能的增加量以及物体克服摩擦力做的功之和 |
| D.物体动能的增加量与物体克服摩擦力做的功之和 |
上题中,若球员将足球以速度v从地面上踢起。其他条件不变(即球门的高度仍为h,足球的质量仍为m,不计空气阻力),取横梁高度处为零势能参考面,则下列说法中正确的是()
A.球员对足球做的功等于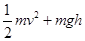 |
B.球员对足球做的功等于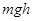 |
C.足球在A点处的机械能为 |
D.足球在B点处的动能为 |