进入21世纪,低碳环保、注重新能源的开发与利用的理念,已经日益融入生产、生活之中。某节水喷灌系统如图所示,喷口距地面的高度h=1.8m,能沿水平方向旋转,喷口离转动中心的距离a=1.0m水可沿水平方向喷出,喷水的最大速率v0=10m/s,每秒喷出水的质量m0=7.0kg。所用的水是从井下抽取的,井中水面离地面的高度H=3.2m,并一直保持不变。水泵由电动机带动,电动机电枢线圈电阻r=5.0Ω。电动机正常工作时,电动机的输入电压U=220V,输入电流I=4.0A。不计电动机的摩擦损耗,电动机的输出功率等于水泵所需要的最大输入功率。水泵的输出功率与输入功率之比称为水泵的抽水效率。(计算时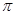 取3,球体表面积公式
取3,球体表面积公式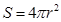 )试求:
)试求: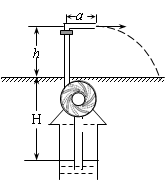
⑴求这个喷灌系统所能喷灌的最大面积S;
⑵假设系统总是以最大喷水速度工作,求水泵的抽水效率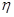 ;
;
⑶假设系统总是以最大喷水速度工作,在某地区将太阳能电池产生的电能直接供该系统使用,根据以下数据求所需太阳能电池板的最小面积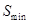 。
。
(已知:太阳光传播到达地面的过程中大约有30%的能量损耗,太阳辐射的总功率 ,太阳到地球的距离
,太阳到地球的距离 ,太阳能电池的能量转化效率约为15%。)
,太阳能电池的能量转化效率约为15%。)
如图所示,固定的斜面长度为2L,倾角为θ,上、下端垂直固定有挡板A、B.质量为m的小滑块,与斜面间的动摩擦因数为μ,最大静摩擦力与滑动摩擦力大小相等,滑块所受的摩擦力大于其重力沿斜面的分力,滑块每次与挡板相碰均无机械能损失.现将滑块由斜面中点P以初速度v0沿斜面向下运动,滑块在整个运动过程与挡板碰撞的总次数为k(k>2),重力加速度为g,试求:
(1)滑块第一次到达挡板时的速度大小v;
(2)滑块上滑过程的加速度大小a和到达挡板B时的动能Ekb;
(3)滑块滑动的总路程s.
如图所示,轻杆的一端用铰链固定在竖直转轴OO′上的O端,另一端固定一小球,轻杆可在竖直平面内自由转动,当转轴以某一角速度匀速转动时,小球在水平面内做匀速圆周转动,此时轻杆与竖直转轴OO′的夹角为37°.已知转轴O端距离水平地面的高度为h,轻杆长度为L,小球的质量为m,重力加速度为g,取sin37°≈0.6,cos37°≈0.8,求: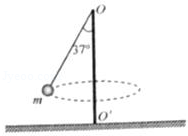
(1)小球做匀速圆周运动的线速度v.
(2)若某时刻小球从轻杆上脱落,小球的落地点到转轴的水平距离d.
(3)若缓慢增大转轴的转速,求轻杆与转轴的夹角从37°增加到53°的过程中,轻杆对小球所做的功W.
如图所示,轨道ABCD位于同一竖直平面内,AB段是光滑的四分之一的圆弧轨道,BC段是高H=3.2m、倾角θ=45°的斜面,CD段是足够长的水平轨道.一小球从AB轨道的某点由静止开始下滑,并从B点水平飞出,不计空气阻力,取g=10m/s2.
(1)若小球从B点飞出后恰好落在C点,求此情形小球在B点的速度大小vB和释放点到B点的高度h0;
(2)若释放点到B点的高度h1=1.8m,求小球第一次落到轨道前瞬间速度方向与水平面夹角α的正切值;
(3)若释放点到B点的高度h2=0.2m,求小球第一次落到轨道的位置到B点的距离L.
如图所示,质量为m的小球以初速度v0= 下落d后,沿竖直平面内的固定轨道ABC运动,AB是半径为d的四分之一粗糙圆弧,BC是半径为
下落d后,沿竖直平面内的固定轨道ABC运动,AB是半径为d的四分之一粗糙圆弧,BC是半径为 的粗糙半圆弧,小球运动到AB圆弧的最低点B时所受弹力大小NB=5mg,且小球恰好能运动到C点,不计空气阻力,重力加速度为g.求:
的粗糙半圆弧,小球运动到AB圆弧的最低点B时所受弹力大小NB=5mg,且小球恰好能运动到C点,不计空气阻力,重力加速度为g.求:
(1)小球在AB圆弧上运动过程中克服摩擦力做的功W1?
(2)小球运动到BC圆弧上C点时的速度大小vC;
(3)小球在圆弧BC上运动过程中,摩擦力对小球做的功W2.
如图所示,长L=3.6m的水平传送带以速度v=2.4m/s匀速运动,小物块P、Q的质量分别为m1=2.0kg、m2=0.5kg,与绕过定滑轮且不可伸长的轻绳相连,t=0时刻P在传送带左端由静止释放,P在传送带上运动时,与定滑轮间的绳保持水平,与传送带间的动摩擦因数μ=0.4,取g=10m/s2,不计定滑轮质量及绳与滑轮间的摩擦,绳足够长,求: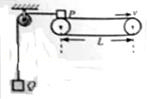
(1)P在传送带上相对滑动时所受滑动摩擦力;
(2)P在传送带上相对滑动时的加速度大小a和绳的拉力大小T;
(3)P在传送带上运动的时间t.