已知：如图，在△ABC中，∠C=90°，∠B=30°，AC=6，点D在边BC上，AD平分∠CAB，E为AC上的一个动点（不与A、C重合），EF⊥AB，垂足为F．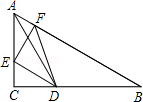
（1）求证：AD=DB；
（2）设CE=x，BF=y，求y关于x的函数解析式；
（3）当∠DEF=90°时，求BF的长？
如图，AB是⊙O的直径，AB=2，半径OC⊥AB于O，以点C为圆心，AC长为半径画弧.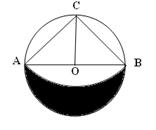
（1）求阴影部分的面积；
（2）把图中以点C为圆心的扇形ACB围成一个圆锥，求这个圆锥的底面半径.
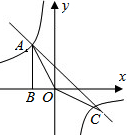
如图，⊿ACO的顶点A，C分别是双曲线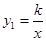
与直线
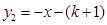在第二象限、第四象限的交点，AB⊥
轴于B且S△ABO=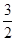
（1）求这两个函数的解析式；
（2）求直线与双曲线的两个交点A，C的坐标；
（3）根据图象写出使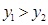
的自变量x的取值范围.
小兵和小宁玩纸牌游戏。下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小兵先从中抽出一张，小宁从剩余的3张牌中也抽出一张。
小宁说：“若抽出的两张牌上的数字都是偶数，你获胜；否则，我获胜。”
（1）请用树状图或列表法表示出抽牌可能出现的所有结果；
（2）若按小宁说的规则进行游戏，这个游戏公平吗？请说明理由。
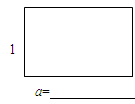
如图, 现有边长为1，a (其中a>1)的一张矩形纸片, 现要将它剪裁出三个小矩形 (大小可以不同， 但不能有剩余), 使每个矩形都与原矩形相似，请在图中画出两种不同裁剪方案的裁剪线的示意图，并直接写出相应的a的值(不必写过程)。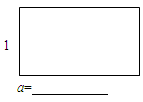
（1）计算：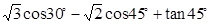
；
（2）已知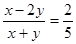
，求
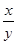的值