为了解决高楼救险中云梯高度不够高的问题，可在消防云梯上再伸出轻便的滑杆。被困人员使用安全带上的挂钩挂在滑杆上、沿滑杆下滑到消防云梯上逃生。通常滑杆由AO、OB两段直杆通过光滑转轴在O处连接，滑杆A端用挂钩钩在高楼的固定物上，且可绕固定物自由转动，B端用铰链固定在云梯上端，且可绕铰链自由转动，以便调节被困人员滑到云梯顶端的速度大小。设被困人员在调整好后的滑杆上下滑时滑杆与竖直方向的夹角保持不变，被困人员可看作质点、不计过O点时的机械能损失。已知AO长L1=6m、OB长L2= 12m、竖直墙与云梯上端点B的水平距离d=13.2m，被困人员安全带上的挂钩与滑杆AO间、滑杆OB间的动摩擦因数均为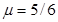
。为了安全被困人员到达云梯顶端B点的速度不能超过6m/s，取g=10m/s2。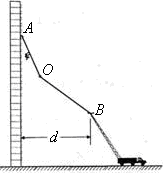
（1）现测得OB与竖直方向的夹角为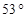
，此时AO与竖直方向的夹角是多少？分析判断这种条件下被困人员滑到B点是否安全。（
，
）
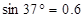（2）若云梯顶端B点与竖直墙间的水平距离保持不变，求能够被安全营救的被困人员与云梯顶端B的最大竖直距离。
如图1所示，质量m=1.0kg的物块，在水平向右、大小F = 5.0N的恒力作用下，沿足够长的粗糙水平面由静止开始运动。在运动过程中，空气对物块的阻力沿水平方向向左，其大小f空=kv，k为比例系数，f空随时间t变化的关系如图2所示。g取10m/s2。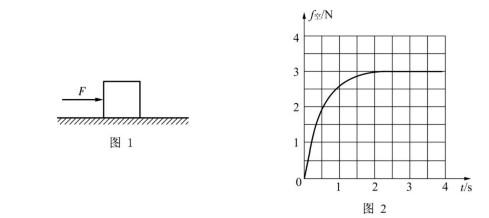
（1）求物块与水平面间的动摩擦因数μ；
（2）估算物块运动的最大速度vm；
（3）估算比例系数k。
现有甲、乙两个小球（可视为质点），它们之间存在大小恒定的引力F。已知甲球质量为3m，乙球质量为m。A、B为光滑水平面上的两点，距离为L。某时刻甲球以向左的速度v0经过A点，同时乙球以向右的速度v0经过B点，求：
（1）甲球加速度的大小；
（2）当两球相距最远时，甲球速度的大小；
（3）甲、乙两球的最大距离。
已知地球半径为R，地球表面处的重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v的表达式；
（2）若已知地球自转的周期为T，求地球同步卫星距离地面的高度h。
如图所示，置于圆形水平转台上的小物块随转台转动。若转台以某一角速度转动时，物块恰好与平台发生相对滑动。现测得小物块与转轴间的距离l=0.50m，小物块与转台间的动摩擦因数μ=0.20，设物块所受的最大静摩擦力等于滑动摩擦力，g取10m/s2。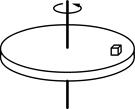
（1）画出小物块随转台匀速转动过程中的受力示意图，并指出提供向心力的力；
（2）求此时小物块的角速度。
如图所示为跳台滑雪的示意图。一名运动员在助滑路段取得高速后从a点以水平初速度v0=15m/s飞出，在空中飞行一段距离后在b点着陆。若测得ab两点的高度差h=20m，不计空气阻力，g取10m/s2，求：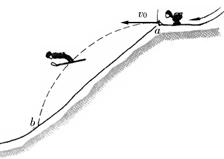
（1）运动员在空中飞行的时间；
（2）运动员在b点着陆前瞬间速度的大小。