如图所示，坐标系xOy在竖直平面内，长为L的水平轨道AB光滑且绝缘，B点坐标为
.有一质量为m、电荷量为＋q的带电小球(可看成质点)被固定在A点．已知在第一象限内分布着互相垂直的匀强电场和匀强磁场，电场方向竖直向上，场强大小E2＝
，磁场为水平方向(在图中垂直纸面向外)，磁感应强度大小为B；在第二象限内分布着沿x轴正方向的水平匀强电场，场强大小E1＝
.现将带电小球从A点由静止释放，设小球所带的电荷量不变．试求：
(1)小球运动到B点时的速度大小；
(2)小球第一次落地点与O点之间的距离；
(3)小球从开始运动到第一次落地所经历的时间．
如图所示，两带电平行板A、B间的电场为匀强电场，场强E=4.0×102V/m，两板相距d=0.16m，板长L=0.30m。一带电量q=1.0×10-16C、质量m=1.0×10-22㎏的粒子沿平行于板方向从两板的正中间射入电场后向着B板偏转，不计带电粒子所受重力，求：
（1）粒子带何种电荷；
（2）要使粒子能飞出电场，粒子飞入电场时的速度v0至少为多大；
（3）粒子飞出电场时最大偏角的正切值
．
如图所示，平行板电容器的两个极板A、B分别接在电压为60 V的恒压电源上，两极板间距为3 cm，电容器带电荷量为6×10－8C，A极板接地（电势为零）．求：
（1）平行板电容器的电容；
（2）平行板电容器两板之间的电场强度；
（3）距B板为2 cm的C点处的电势．
如图所示，在场强大小为E的匀强电场中，将电荷量为+q的点电荷由A点沿直线移至B点，AB间的距离为L，AB方向与电场方向成60°角，求：
（1）点电荷所受电场力的大小；
（2）在此过程中电场力做的功；
（3）A、B两点间的电势差。
如图所示，把一带电量为-5×10-8C的小球A用绝缘细绳悬起，若将带电量为 +4×10-6C的带电小球B靠近A，当两个带电小球在同一高度相距30cm时，绳与竖直方向成45°角，取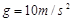
，
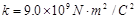，且A、B两小球均可视为点电荷, 求：
（1）AB两球间的库仑力；
（2）A球的质量．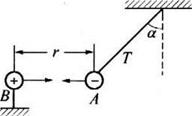
雨点下落过程中受到的空气阻力与雨点的横截面积成正比，与下落的速度平方成正比，即Ff=kSv2(k是比例常数，S=πr2)，若雨点看作球形，其半径为r，球的体积为4πr3/3．雨点的密度为ρ，每个雨点最终都做匀速运动．试通过推理，推导出雨点最终速度与雨点半径r的关系．