如果质点所受的力与它偏离平衡位置位移的大小成正比，并且总是指向平衡位置，即F=-kx，其中k是由系统本身特性决定的线性回复力常数，那么质点的运动就是简谐运动。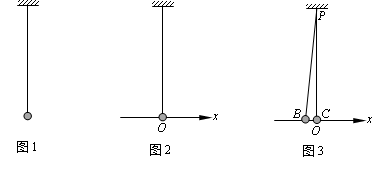
（1）图1所示为一理想单摆，摆球的质量为m，摆长为L。重力加速度为g。请通过计算说明该单摆做简谐运动的线性回复力常数k=?
（2）单摆做简谐运动的过程中，由于偏角很小，因此可以认为摆球沿水平直线运动。
如图2所示，质量为m的摆球在回复力F=-kx作用下沿水平的x轴做简谐运动，若振幅为A，在平衡位置O点的速度为vm，试证明：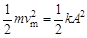
。
（3）如图3所示，两个相同的理想单摆均悬挂在P点。将B球向左拉开很小的一段距离由静止释放，B球沿水平的x轴运动，在平衡位置O点与静止的C球发生对心碰撞，碰撞后B、C粘在一起向右运动。已知摆球的质量为m，摆长为L。释放B球时的位置到O点的距离为d。重力加速度为g。求B、C碰撞后它们沿x轴正方向运动的最大距离。
如图所示，水平面上有一重为40N的物体，受到F1=13N和F2=6N的水平力作用而保持静止，已知物体与水平面间的动摩擦因数μ=0.2，设最大的静摩擦力等于滑动摩擦力．求：
（1）物体所受摩擦力的大小和方向．
（2）若只撤去F1，物体所受摩擦力的大小和方向．
（3）若只撤去F2，物体所受摩擦力的大小和方向．
一辆汽车正以v0=30m/s的速度在平直路面上行驶，驾驶员突然发现正前方约50m处有一个障碍物，立即以大小为8m/s2的加速度刹车。为了研究汽车经过2s是否撞上障碍物，甲、乙两位同学根据已知条件作出以下判断：
甲同学认为汽车已撞上障碍物，理由是：
在2s时间内汽车通过的位移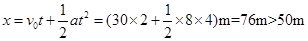
乙同学也认为汽车已撞上障碍物，理由是：
在2s时间内汽车通过的位移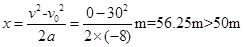
问：以上两位同学的判断是否正确？如果不正确，请指出错误的原因，并作出正确的解答。
如图所示，真空有一个半径r="0.5" m的圆形磁场，与坐标原点相切,磁场的磁感应强度大小B=2×10-3 T,方向垂直于纸面向里，在x=r处的虚线右侧有一个方向竖直向上的宽度为L1="0.5" m的匀强电场区域，电场强度E=1.5×103 N/C。在x="2" m处有一垂直x方向的足够长的荧光屏，从O点处向不同方向发射出速率相同的荷质比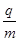
=1×109 C/kg带正电的粒子，粒子的运动轨迹在纸面内，一个速度方向沿y轴正方向射入磁场的粒子，恰能从磁场与电场的相切处进入电场。不计重力及阻力的作用。求：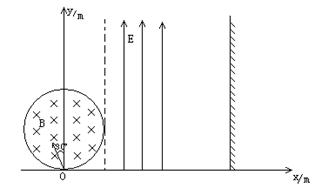
（1）粒子进入电场时的速度和沿y轴正方向射入的粒子在磁场中运动的时间？
（2）从O点入射的所有粒子经磁场偏转后出射的速度方向有何特点？请说明理由。
（3）速度方向与y轴正方向成30°（如图中所示）射入磁场的粒子，最后打到荧光屏上，该发光点的位置坐标。
某学校探究性学习小组对一辆自制小遥控车的性能进行研究．他们让这辆小车在水平的地面上由静止开始运动，并将小车运动的全过程记录下来，通过数据处理得到如图所示的v－t图象，已知小车在0～2 s内做匀加速直线运动，2～10 s内小车牵引力的功率保持不变，在10 s末停止遥控让小车自由滑行，小车质量m＝1 kg，整个过程中小车受到的阻力大小不变．求：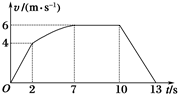
(1)小车所受的阻力Ff是多大？
(2)在2～10 s内小车牵引力的功率P是多大？
(3)小车在加速运动过程中的总位移x是多少？
半径R＝0.50 m的光滑圆环固定在竖直平面内，轻质弹簧的一端固定在环的最高点A处，另一端系一个质量m＝0.20 kg的小球，小球套在圆环上，已知弹簧的原长为L0＝0.50 m，劲度系数k＝4.8 N/m，将小球从如图所示的位置由静止开始释放，小球将沿圆环滑动并通过最低点C，在C点时弹簧的弹性势能EPC＝0.6 J，g取10 m/s2.求：
(1)小球经过C点时的速度vc的大小；
(2)小球经过C点时对环的作用力的大小和方向．