已知⊙O及⊙O外一点P，过点P作出⊙O的一条切线（只有圆规和三角板这两种工具）．以下是甲、乙两同学的作业：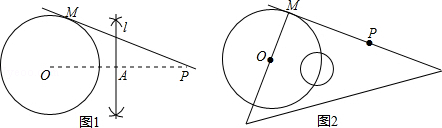
甲：①连接OP，作OP的垂直平分线l，交OP于点A；
②以点A为圆心、OA为半径画弧、交⊙O于点M；
③作直线PM，则直线PM即为所求（如图1）．
乙：①让直角三角板的一条直角边始终经过点P；
②调整直角三角板的位置，让它的另一条直角边过圆心O，直角顶点落在⊙O上，记这时直角顶点的位置为点M；
③作直线PM，则直线PM即为所求（如图2）．
对于两人的作业，下列说法正确的是（ ）
| A．甲对，乙不对 | B．甲不对，乙对 | C．两人都对 | D．两人都不对 |
的算术平方根，即
的解集在数轴上的表示是 ( )
与下列哪个方程组合，使得方程组的解是
（）
的解是( )
