如图,设∠BAC=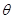 (0°<
(0°<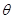 <90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点
<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点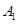 开始,用等长的小棒依次向右摆放,其中
开始,用等长的小棒依次向右摆放,其中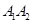 为第一根小棒,且
为第一根小棒,且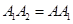 .
.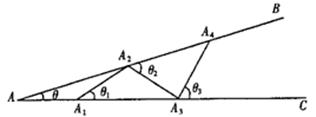
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则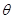 1 =___________,
1 =___________,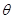 2=__________,
2=__________, 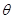 3=__________;(用含
3=__________;(用含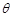 的式子表示)
的式子表示)
(3)若只能摆放4根小棒,求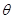 的范围.
的范围.
如图,AB是⊙O的直径,AC是弦.
(1)请你按下面步骤画图;
第一步,过点A作∠BAC的角平分线,交⊙O于点D;
第二步,过点D作AC的垂线,交AC的延长线点E.
第三步,连接BD.
(2)求证:AD2=AE•AB;
(3)连接EO,交AD于点F,若5AC=3AB,求 的值.
的值.
先阅读下面的材料,然后解答问题:通过观察,发现方程 的解为
的解为 ;
; 的解为
的解为 ;
; 的解为
的解为 ;
;
…………………………
(1)观察上述方程的解,猜想关于x的方程 的解是________________;
的解是________________;
(2)根据上面的规律,猜想关于x的方程 的解是___________________;
的解是___________________;
(3)把关于x的方程 变形为方程
变形为方程 的形式是______,方程的解是___________.
的形式是______,方程的解是___________.
2012年5月18日,某国3艘炮艇追袭5条中国渔船.刚刚完成黄岩岛护渔任务的“中国渔政310”船人船未歇立即追往北纬11度22分、东经110度45分附近海域护渔,保护100多名中国渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.
解决问题:如图,已知“中国渔政310”船(A)接到陆地指挥中心(B)命令时,渔船(C)位于陆地指挥中心正南方向,位于“中国渔政310”船西南方向,“中国渔政310”船位于陆地指挥中心南偏东60°方向,AB=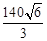 海里,“中国渔政310”船最大航速20海里/时.根据以上信息,请你求出“中国渔政310”船赶往出事地点需要多少时间.
海里,“中国渔政310”船最大航速20海里/时.根据以上信息,请你求出“中国渔政310”船赶往出事地点需要多少时间.
正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM;
(2)当AE=1时,求EF的长.
已知一次函数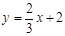 的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数
的图象分别与坐标轴相交于A、B两点(如图所示),与反比例函数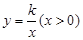 的图象相交于C点.
的图象相交于C点.
(1)写出A、B两点的坐标;
(2)作CD⊥x轴,垂足为D,如果OB是△ACD的中位线,求反比例函数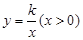 的关系式.
的关系式.