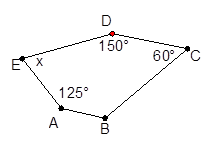如图，已知A（-4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数
的图象的两个交点． 
（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．
先化简、再求值：
，其中a＝
－3．
如图（1），由三角形的内角和或外角和可知：∠ABC=∠A+∠C+∠O
在图（2）中，直接利用上述的结论探究：
①AD、CD分别平分∠OAB，∠OCB，且∠O=80°∠B=120°，求∠ADC的度数
②AD、CD分别平分∠OAB，∠OCB，猜想∠O，∠ABC，∠ADC之间的等量关系，并说明理由。
RT△ABC沿AB的方向平移AD距离得△DEF。已经BE=4,EF=8,CG=3,求图中阴影部分的面积。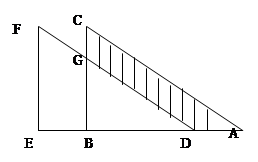
有一艘渔船上午九点在A处沿正东方向航行，在A处测得灯塔C在北偏东60°方向上，行驶2小时到达B处，测得灯塔C在北偏东15°方向，求∠C的度数。
已知：如图，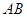
// 
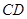，求图形中的x的值.