阅读下面的材料：
小明在学习中遇到这样一个问题：若1≤x≤m，求二次函数
的最大值．他画图研究后发现，
和
时的函数值相等，于是他认为需要对
进行分类讨论．他的解答过程如下：
∵二次函数的对称轴为直线
，
∴由对称性可知，和时的函数值相等．
∴若1≤m＜5，则时，
的最大值为2；
若m≥5，则
时，的最大值为
．
请你参考小明的思路，解答下列问题：
（1）当
≤x≤4时，二次函数
的最大值为_______；
（2）若p≤x≤2，求二次函数的最大值；
（3）若t≤x≤t+2时，二次函数的最大值为31，则
的值为_______．
雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=
AB，AF=AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由。
在平面直角坐标系xOy中，已知直线l1经过点A(-2，0)和点B(0，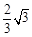
)，直线l2的函数表达式为
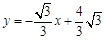，l1与l2相交于点P．⊙C是一个动圆，圆心C在直线l1上运动，设圆心C的横坐标是a．过点C作CM⊥x轴，垂足是点M．求直线l1的函数表达式；
当⊙C和直线l2相切时，请证明点P到直线CM的距离等于⊙C的半径R，并写出R=
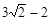时a的值.当⊙C和直线l2不相离时，已知⊙C的
半径R=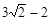，记四边形NMOB的面积为S(其中点N是直线CM与l2的交点)．S是否存在最大值？若存在，求出这个最大值及此时a的值；若不存在，请说明理由．
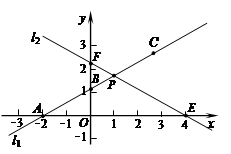
如图，点
、
、
是
上的三点，
.求证：
平分
.
过点
作
于点
，交
于点
. 若
，
，求
的长．
）如果关于
的方程
没有实数根，试判断关于
的方程
的根的情况.
某电厂规定,该厂家家属区每户居民如果一个月的用电量不超过A度,那么这个居民这个月只需交10元电费；如果超过A度，则这个月除了仍要交10元电费以外，超过的部分还要每度按
交费.该厂某户居民2月份用电90度,超过了规定的A度,则超过的部分应交电费元(用A表示)；
下表是这户居民3月、4月用电情况和交费情况：
| 月份 |
用电量（度） |
交点费总数（元） |
| 3 |
80 |
25 |
| 4 |
45 |
10 |
根据上表数据，求出电厂规定的A值.