如图所示，在匀强磁场中有一倾斜的光滑平行金属导轨，导轨间距为L=1m，导轨长为d=3m，导轨平面与水平面的夹角为θ＝300，匀强磁场的磁感应强度大小为B＝1T，方向与导轨平面垂直向上，质量为m＝0.1Kg的导体棒从导轨的顶端由静止开始释放，导棒在滑至底端之前已经做匀速运动，设导体棒始终与导轨垂直，并与导轨接触良好，接在两导轨间的电阻为R=2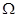
，其他部分的电阻均不计，重力加速度g=10m/s2。求：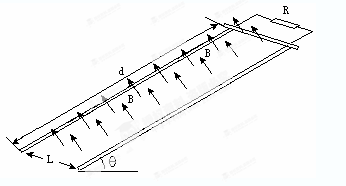
(1)导体棒匀速运动时的速度v大小；
(2)导体棒从导轨的顶端运动到底端的整个过程中，电阻R产生的焦耳热Q。
如图中实线是一列简谐横波在t1＝0时刻的波形，虚线是这列波在t2＝0.5 s时刻的波形，这列波的周期T符合：3T<t2－t1<4T.问：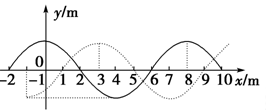
(1)若波速向右，波速多大？
(2)若波速向左，波速多大？
一列简谐横波沿x轴正方向传播，t＝0时刻的波形如图所示，介质中质点P、Q分别位于x＝2m、x＝4m处．从t＝0时刻开始计时，当t＝15 s时质点Q刚好第4次到达波峰．
(1)求波速；
(2)写出质点P做简谐运动的表达式(不要求推导过程)．
汽车的车身是装在弹簧上的，如果这个系统的固有周期是1.5 s，汽车在一条起伏不平的路上行驶，路上各凸起处大约都相隔8 m，汽车以多大速度行驶时，车身上下颠簸得最剧烈？
如图为某种透明材料制成的边长为4cm，横截面为正三角形的三棱镜，将其置于空气中，当一细光束从距离顶点A为1cm的D点垂直于AB面入射时，在AC面上刚好发生全反射，光在真空中的速度c=3×108m/s。求：
①此透明材料的折射率；②光通过三棱镜的时间。
一气象探测气球，在充有压强为1.00atm（即76.0cmHg）、温度为
的氦气时，体积为4.5m3。在缓慢上升至海拔6.0km高空的过程中，气球内氦气压强逐渐减小到此高度上的大气压38.0cmHg，气球内部因启动一持续加热过程而维持其温度不变。此后停止加热，保持高度不变。已知在这一海拔高度气温为
。求：
（1）氦气在停止加热前的体积
（2）氦气在停止加热较长一段时间后的体积。