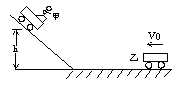
在民航业内,一直有“黑色10分钟”的说法,即从全球已发生的飞机事故统计数据来看,大多数的航班事故发生在飞机起飞阶段的3分钟和着陆阶段的7分钟。飞机安全事故虽然可怕,但只要沉着冷静,充分利用逃生设备,逃生成功概率相当高,飞机失事后的90秒内是逃生的黄金时间。如图为飞机逃生用的充气滑梯,滑梯可视为理想斜面,已知斜面长L=8m,斜面倾斜角θ=37°,人下滑时与充气滑梯间动摩擦因素为 =0.5。不计空气阻力,g=10m/s2,Sin37°=0.6,cos37°=0.8, 求:
=0.5。不计空气阻力,g=10m/s2,Sin37°=0.6,cos37°=0.8, 求:
(1)旅客从静止开始由滑梯顶端滑到底端逃生,需要多长时间?
(2)一旅客若以V0=4.0m/s的初速度抱头从舱门处水平逃生,当他落到充气滑梯上后没有反弹,由于有能量损失,结果他以v=4.0m/s的速度开始沿着滑梯加速下滑。该旅客以这种方式逃生与(1)问中逃生方式相比,节约了多长时间?
如图,物体A质量m=2.0Kg放在粗糙木板上,随板一起在竖直平面内做半径r=0.4m,沿逆时针方向匀速圆周运动,且板始终保持水平,当板运动到最高点时,木板受到物体A的压力恰好为零,重力加速度为g=10m/s2.求:
(1)物体A做匀速圆周运动的线速度大小.
(2)物体A运动到最低点时,木板对物体A的支持力大小.
如图所示,一光滑的半径为R的竖直半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,当小球将要从水平轨道口B飞出时,球对轨道的压力恰好为mg。求: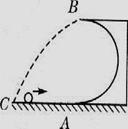
(1)、小球从水平轨道口B飞出时速度是多少m/s 。
(2)、小球落地点C距A(A在B的正下方)处多远。
(重力加速度为g)
一个3kg的物体在半径为2m的圆周上以4m/s的速度运动,向心加速度是多大?所需向心力是多大?
一颗人造地球卫星距地面的高度为h,地球半径为R,地球表面处的重力加速度为g,求该卫星的线速度的大小。
如图所示,甲车质量m1=20kg,车上有质量M=50kg的人,甲车(连同车上的人)从足够长的斜坡上高h=0.45m由静止滑下,到水平面上后继续向前滑动。此时质量m2=50kg的乙车正以v0=1.8m/s的速度迎面滑来,为了避免两车相撞,当两车相距适当距离时,人从甲车跳到乙车上,求人跳出甲车的水平速度(相对地面)应在什么范围以内?不计地面和斜坡的摩擦,取g=10m/s2。