某校计划开设4门选修课:音乐、绘画、体育、舞蹈,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门),对调查结果进行统计后,绘制了如下不完整的两个统计图.
根据以上统计图提供的信息,回答下列问题:
(1)此次调查抽取的学生人数为a= 人,其中选择“绘画”的学生人数占抽样人数的百分比为b= ;
(2)补全条形统计图;
(3)若该校有2000名学生,请估计全校选择“绘画”的学生大约有多少人?
化简求值: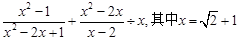 .
.
在平面直角坐标系中,二次函数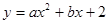 的图象与
的图象与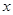 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.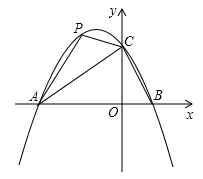
(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于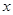 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.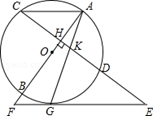
(1)求证:KE=GE;
(2)若AC∥EF,试判断线段KG、KD、GE间的相等
数量关系,并说明理由;
(3)在(2)的条件下,若sinE=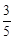 ,AK=
,AK=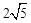 ,求FG的长.
,求FG的长.
某仓库有甲种货物360吨,乙种货物290吨,计划用A、B两种共50辆货车运往外地.已知一辆A种货车的运费需0.5万元,一辆B种货车的运费需0.8万元.
(1)设A种货车为 辆,运输这批货物的总运费为y万元,试写出y与
辆,运输这批货物的总运费为y万元,试写出y与 的关系表达式;
的关系表达式;
(2)若一辆A种货车能装载甲种货物9吨和乙种货物3吨;一辆B种货车能装载甲种货物6吨和乙种货物8吨.按此要求安排A,B两种货车运送这批货物,有哪几种运输方案?请设计出来;
(3)试说明哪种方案总运费最少?最少运费是多少万元?
如图1,在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD= ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
图1
(1)求证:CF=CH;
(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE= 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.
图2