九年级某班同学在毕业晚会中进行抽奖活动,在一个不透明的口袋中有三个完全相同的小球,把它们分别标号为1,2,3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一样),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
(本题12分) 某水果批发商场经销一种水果,如果每千克盈利10元,每天可售出400千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)当每千克涨价为多少元时,每天的盈利最多?最多是多少?
(2)若商场只要求保证每天的盈利为4420元,同时又可使顾客得到实惠,每千克应涨价为多少元?
(本题10分)如图,在⊙O中,弧AB=60°,AB=6,
(1)求圆的半径;
(2)求弧AB的长;
(3)求阴影部分的面积.
(本题10分)二次函数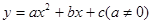 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出方程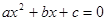 的两个根;
的两个根;
(2)当x为何值时,y>0;y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.
(本题10分)如图,函数 的图象与函数
的图象与函数 (
( )的图象交于A(
)的图象交于A( ,1)B(1,
,1)B(1, )两点.
)两点.
(1)求函数 的表达式;
的表达式;
(2)观察图象,比较当 时,
时, 与
与 的大小.
的大小.
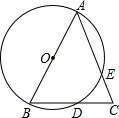
(本题8分)已知:如图,在△ABC中,AB为⊙O的直径,BC,AC分别交⊙O于D、E两点,若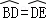 ,求证:AB=AC
,求证:AB=AC