某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
在平面直角坐标系中,抛物线y=x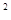 +5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
+5x+4的顶点为M,与x轴交于A、B两点与y轴交于C点。
(1)求点A、B、C的坐标;
(2)求抛物线y=x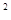 +5x+4关于坐标原点O对称的抛物线的函数表达式;
+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为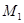 ,与x轴交于
,与x轴交于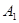 、
、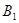 两点,与y轴交于
两点,与y轴交于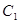 点,在以A、B、C、M、
点,在以A、B、C、M、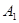 、
、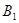 、
、 、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
、、这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积。
如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E。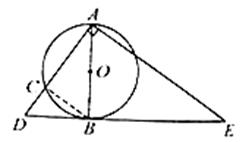
(1)求证:∠BAD=∠E;
(2)若⊙O的半径为5,AC=8,求BE的长。
某中学要在全校学生中举办“中国梦·我的梦”主题演讲比赛,要求每班一
名代表参赛,九年级(1)班经过投票初选,小亮和小丽票数并列班级第一,现在他们都想代表本班参赛,
经班长与他们协商决定,用他们学过的掷骰子游戏来确定谁去参赛(胜者参赛)。规则如下:两人同时随机
各掷一枚完全相同且质地均匀的骰子一次,向上一面的点数都是奇数,则小亮胜;向上一面的点数都是偶
数,则小丽胜;否则,视为平局,若为平局,继续上述游戏,直至分出胜负为止。如果小亮和小丽按上述
规则各掷一次骰子,那么请你解答下列问题:
(1)小亮掷得向上一面的点数为奇数的概率是多少?
(2)该游戏是否公平?请用列表或树状图等方法说明理由。(骰子:六个面上分别刻有1、2、3、4、5、6 个小圆点的小正方体)
胡老师计划组织朋友暑假去革命圣地延安两日游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团两日游的游客,甲旅行社表示,每人都按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费。假设组团参加甲、乙两家旅行社两日游的人数均为x人。
(1)请分别写出甲、乙两家旅行社收取组团两日游的总费用y(元)与x(人)之间的函数
关系式;
(2)若胡老师组团参加两日游的人数共有32人,请你通过计算,在甲、乙两家旅行社中,
帮助胡老师选择收取总费用较少的一家。
晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高,于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长,已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ,请你根据以上信息,求出小军身高BE的长(结果精确到0.01米)