如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为18°,且OA=OB=3m.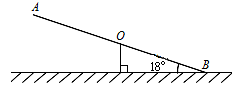
(1)求此时另一端A离地面的距离(结果精确到0.1);
(2)跷动AB,使端点A碰到地面,请画出点A运动的路线(保留画图痕迹),并求出点A运动路线的长.(结果保留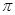 )(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
(1)计算: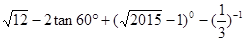 ;
;
(2)化简: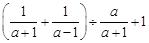 .
.
如图,抛物线y=ax2+bx(a>0)与双曲线y= 相交于点A,B.已知点B的坐标为(﹣2,﹣2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.
相交于点A,B.已知点B的坐标为(﹣2,﹣2),点A在第一象限内,且tan∠AOx=4.过点A作直线AC∥x轴,交抛物线于另一点C.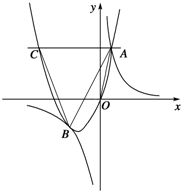
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积.若存在,请你写出点D的坐标;若不存在,请你说明理由.
如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连结PD,过点P作PQ⊥PD,交直线BC于点Q.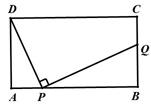
(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;
(2)连结AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示)
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.