数学课上,李老师出示了如下的题目:
“在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图,试确定线段AE与DB的大小关系,并说明理由”.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图①,确定线段AE与DB的大小关系,请你直接写出结论:
AE ______ DB(填“>”,“<”或“=”).
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE _____ DB(填“>”,“<”或“=”).
理由如下:
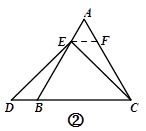
如图②,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)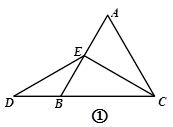
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为2,AE=1,求CD的长(请你直接写出结果).
如图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),白棋③的坐标是(-1,-3),则黑棋②的坐标是 .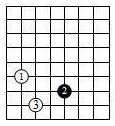
如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在南北向的公路上确定点P,使得△PAB是等腰三角形,则这样的点P最多能确定 个.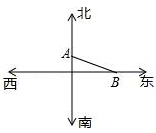
从A地到B地的距离为60千米,一辆摩托车以平均每小时30千米的速度从A地出发到B地,则摩托车距B地的距离s(千米)与行驶时间t(时)的函数表达式为 .
一等腰三角形的腰长为15,底边长为18,则它底边上的高为 cm.
如图,已知Rt△ABC中,∠ACB=90°,D是AB的中点,CD=2cm,则AB= cm.