直线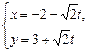 (t为参数)上与点P(-2,3)的距离等于
(t为参数)上与点P(-2,3)的距离等于 的点的坐标是
的点的坐标是
| A.(-4,5) | B.(-3,4) |
| C.(-3,4)或(-1,2) | D.(-4,5)或(0,1) |
下列命题中不正确的是
| A.若A+B+C=0,则直线Ax+By+C=0必过定点 |
| B.直线Ax+By+C=0与Bx-Ay+C=0恒有交点 |
C.设A·B≠0,过定点(x0,y0)且与直线Ax+By+C=0垂直的直线的方程是 = = |
| D.过点(2,3)且在两坐标轴上的截距的绝对值相等的直线有且只有两条 |
曲线f(x,y)=0关于直线x-y-2=0对称的曲线方程是
| A.f(y+2,x)="0" | B.f(x-2,y)=0 |
| C.f(y+2,x-2)="0" | D.f(y-2,x+2)=0 |
直线2x-y-4=0绕着它与x轴的交点,按逆时针方向旋转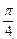 后,所得的直线方程是
后,所得的直线方程是
| A.x-3y-2="0" | B.3x+y-6=0 |
| C.3x-y+6="0" | D.x-y-2=0 |
△ABC三顶点坐标为A(2,2)、B(-2,-2)、C(2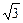 ,-2
,-2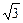 ),则此三角形是
),则此三角形是
| A.等边三角形 | B.直角三角形 |
| C.等腰三角形 | D.钝角三角形 |