(本小题满分14分)若数列 的前
的前 项和为
项和为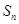 ,对任意正整数
,对任意正整数 ,都有
,都有 ,记
,记 .
.
(1)求 ,
,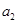 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)令 ,数列
,数列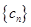 的前
的前 项和为
项和为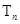 ,证明:对于任意的
,证明:对于任意的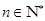 ,都有
,都有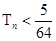 .
.
已知A(2,3),B(1,4),C(6,9),D(10,11),证明:四边形ABCD是直角梯形。 (12分)
已知A(1,-1),B(3,3),C(4,5),试问A、B、C三点是否在同一条直线上?请说明理由。
((本小题满分12分)
已知点F(1,0),直线 ,设动点P到直线
,设动点P到直线 的距离为
的距离为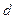 ,已知
,已知 ,且
,且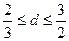 .
.
(1)求动点P的轨迹方程;
(2)若 ,求向量
,求向量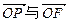 的夹角;
的夹角;
(3)如图所示,若点G满足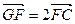 ,点M满足
,点M满足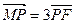 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求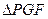 的面积.
的面积.
((本小题满分12分)
已知函数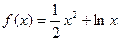 .
.
(1)求函数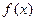 在区间
在区间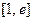 上的最大值、最小值;
上的最大值、最小值;
(2)已知 ,求证:在区间
,求证:在区间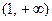 上,函数
上,函数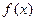 的图象在函数
的图象在函数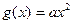 的图象的下方.
的图象的下方.
((本小题满分12分)
数列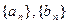 满足:
满足: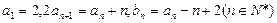
(1)求数列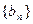 的通项公式;
的通项公式;
(2)设数列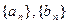 的前n项和分别为An、Bn,问是否存在实数
的前n项和分别为An、Bn,问是否存在实数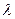 ,使得
,使得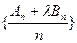 为等差数列?若存在,求出
为等差数列?若存在,求出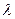 的值;若不存在,说明理由。
的值;若不存在,说明理由。