如图所示，固定不动的足够长斜面倾角θ＝37°，一个物体以v0＝12 m/s的初速度，从斜面A点处开始自行沿斜面向上运动，加速度大小为a＝8.0 m/s2。
(g="10" m/s2，sin 37°＝0.6，cos 37°＝0.8)求：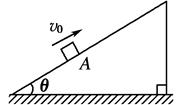
（1）物体沿斜面上升的最大距离；
（2）画出物体沿斜面上升的受力分析图，求出物体与斜面间动摩擦因数；
（3）据条件判断物体上升到最高点后能否返回？若能，求返回时的加速度。
如图所示,PQ是一固定在水平地面上足够长的绝缘平板（右侧有挡板）,整个空间有平行于平板向左、场强为E的匀强电场,在板上C点的右侧有一个垂直于纸面向里、磁感应强度为B的匀强磁场.一个质量为m,电荷量为q的小物块,从C点由静止开始向右先做加速运动再做匀速运动.当物体碰到右端挡板后被弹回,若在碰撞瞬间撤去电场,小物块返回时在磁场中恰做匀速运动.已知平板QC部分的长度为L,物块与平板间的动摩擦因数为μ求:
（1）判断物块的电性；
（2）小物块向右运动过程中克服摩擦力做的功；
（3）小物块与右端挡板碰撞过程损失的机械能。
如图所示的坐标平面内,在y轴的左侧存在垂直纸面向外、磁感应强度大小B1=0.20T的匀强磁场,在y轴的右侧存在垂直纸面向里、宽度d=0.125m的匀强磁场B2.某时刻一质量m=2.0×10-8kg、电量q=+4.0×10-4C的带电微粒（重力可忽略不计）,从x轴上坐标为（-0.25m,0）的P点以速度v=2.0×103 m/s沿y轴正方向运动.试求:
（1）微粒在y轴的左侧磁场中运动的轨道半径;
（2）微粒第一次经过y轴时速度方向与y轴正方向的夹角;
（3）要使微粒不能从右侧磁场边界飞出,B2应满足的条件
如图所示，只有在
的区域中，存在着垂直于纸面的、磁感应强度为B0的匀强磁场，一个质量为m、带电量为
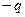的带电粒子（不计重力），从坐标原点O以初速度
沿着与
轴正向成300角的方向垂直于磁场方向进入。求该带电粒子离开磁场的位置以及方向。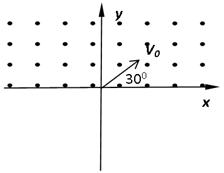
有一个带电量q = −3.2×10-19C的点电荷,从电场中的A点移到B点时,克服电场力做功12.8×10-19 J,从B点移到C点时,电场力做功16×10-19 J｡求:
（1）A、B、C三点之间的电势差UAB、UBC和UCA各是多少?
（2）若规定B点电势为零,则A、C两点的电势φA和φC各是多少?
如图所示，板长为L的平行板电容器倾斜固定放置，极板与水平线夹角θ=300，某时刻一质量为m，带电量为q的小球由正中央A点静止释放，小球离开电场时速度是水平的，落到距离A点高度为h的水平面处的B点，B点放置一绝缘弹性平板M，当平板与水平夹角a=450时，小球恰好沿原路返回A点．求：
（1）电容器极板间的电场强度；
（2）平行板电容器的板长L；
（3）小球在AB间运动的周期．