(本小题满分10分)选修4-4:坐标系与参数方程
以平面直角坐标系的原点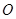 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点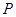 的直角坐标
的直角坐标
为(1,-5),点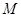 的极坐标为(4,
的极坐标为(4,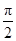 ),若直线
),若直线 过点
过点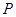 ,且倾斜角为
,且倾斜角为 ,
,
圆 以
以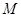 为圆心,4为半径.
为圆心,4为半径.
(1)求直线 的参数方程和圆
的参数方程和圆 的极坐标方程;
的极坐标方程;
(2)试判定直线 与圆
与圆 的位置关系.
的位置关系.
已知向量 ,
, ,
,
(Ⅰ)若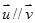 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 ,求实数
,求实数 的值。
的值。
已知实数集R,集合 ,集合
,集合 ,集合
,集合 .
.
(Ⅰ)求 (C
(C ;
;
(Ⅱ)若 ,求
,求 的取值范围。
的取值范围。
已知函数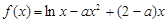 .
.
(1)讨论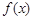 的单调性;
的单调性;
(2)设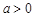 ,证明:当
,证明:当 时,
时, ;
;
(3)若函数 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: (x0)<0.
(x0)<0.
已知平面上的线段l及点P,在l上任取一点Q,线段PQ长度的最小值称为点P到线段l的距离,记作 。
。
(1)已知点 ,线段
,线段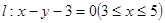 ,求
,求 ;
;
(2)设A(-1,0),B(1,0),求点集 所表示图形的面积;
所表示图形的面积;
(3)若M(0,1),O(0,0),N(2,0),画出集合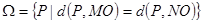 所表示的图形。
所表示的图形。
把正奇数数列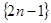 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
35
7 9 11
………………………
……………………………
设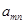
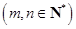 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第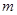 行、从左往右数第
行、从左往右数第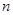 个数.
个数.
(1)若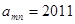 ,求
,求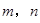 的值;
的值;
(2)若记三角形数表中从上往下数第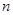 行各数的和为
行各数的和为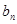 ,求证
,求证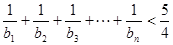 .
.