在平面直角坐标系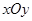 中,已知圆
中,已知圆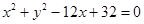 的圆心为
的圆心为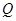 ,过点P(0,2)且斜率为k的直线与圆
,过点P(0,2)且斜率为k的直线与圆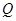 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求k的取值范围;
(2)是否存在常数k,使得向量 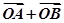 与
与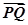 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.
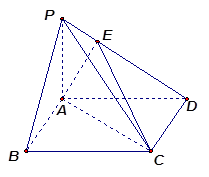
如图,在四棱锥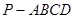 中,底面
中,底面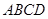 是边长为
是边长为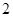 的正方形,
的正方形,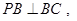
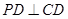 ,且
,且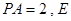 点满足
点满足 .
. 
(1)证明: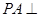 平面
平面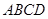 .
.
(2)在线段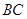 上是否存在点
上是否存在点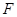 ,使得
,使得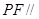 平面
平面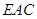 ?若存在,确定点
?若存在,确定点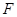 的位置,若不存在请说明理由 .
的位置,若不存在请说明理由 .
已知一个几何体的三视图(单位:cm)如图所示,求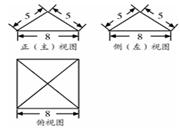
(1)该几何体的体积
(2)该几何体的表面积
已知集合 ,
, ,且
,且 ,求
,求
已知椭圆的中心为坐标原点O,焦点在x轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点, 与
与 =(3,-1)共线.
=(3,-1)共线.
(1)求椭圆的离心率;
(2)设M为椭圆上任意一点,且 (
( ),证明
),证明 为定值.
为定值.
如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,M是PD的中点.
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成角的正弦值;
(3)以AC的中点O为球心、AC为直径的球交PC于点N求点N到平面ACM的距离.