已知椭圆的焦点坐标是
，
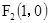，过点
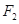垂直于长轴的直线交椭圆与
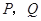两点, 且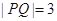
.
（1）求椭圆的方程.
（2）过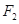的直线与椭圆交于不同的两点
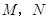, 则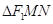
的内切圆面积是否存在最大值?若存在, 则求出这个最大值及此时的直线方程; 若不存在,请说明理由.
已知函数
（Ⅰ）若函数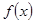
恰好有两个不同的零点，求
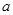的值。
（Ⅱ）若函数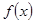的图象与直线
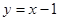相切，求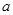的值及相应的切点坐标。
已知
,
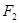是椭圆
左右焦点，它的离心率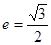
，且被直线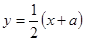
所截得的线段的中点的横坐标为
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设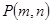
是其椭圆上的任意一点，当
为钝角时，求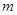
的取值范围。
已知函数f(x)＝cos(2x＋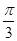
)＋
－
＋
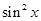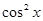sinx·cosx
⑴ 求函数f(x)的单调减区间；⑵ 若xÎ[0,
]，求f(x)的最值；
⑶ 若f(a)＝
，2a是第一象限角，求sin2a的值.
在△ABC中，a、b、c分别是角A、B、C的对边,cosB＝
.
⑴ 若cosA＝－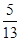
,求cosC的值；⑵ 若AC＝
,BC＝5，求△ABC的面积.
⑴ 求
－
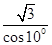的值；
⑵ 已知tana＝3,求
的值.