如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是()cm2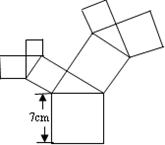
| A.28 | B.49 | C.98 | D.147 |
将一些完全相同的梅花按如图所示的规律摆放,第1个图形有5朵梅花,第2个图形有8朵梅花,第3个图形有13朵梅花,…,按此规律,则第11个图形中共有梅花的朵数是()
| A.121 | B.125 | C.144 | D.148 |
如图,小方格都是边长为1的正方形,则四边形ABCD的面积是()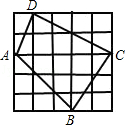
| A.25 | B.12.5 | C.9 | D.8.5 |
平行四边形、矩形、菱形、等腰三角形、正方形中是轴对称图形的有()个
| A.1 | B.2 | C.3 | D.4 |
已知正方形的边长为4cm,则其对角线长是()
| A.8cm | B.16cm | C.32cm | D. cm cm |