(本小题满分13分)已知椭圆的焦点在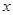 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线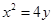 的焦点,离心率
的焦点,离心率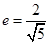 .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点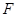 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线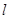 ,交椭圆于
,交椭圆于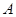 、
、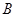 两点,设点
两点,设点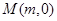 是线段
是线段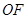 上的一个动点,且
上的一个动点,且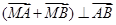 ,求
,求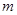 的取值范围;
的取值范围;
(3)设点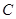 是点
是点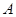 关于
关于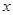 轴的对称点,在
轴的对称点,在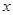 轴上是否存在一个定点
轴上是否存在一个定点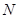 ,使得
,使得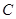 、
、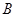 、
、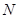 三点共线?若存
三点共线?若存
在,求出定点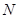 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
某班共有24人参加同时开设的数学兴趣小组和物理兴趣小组,其中参加数学兴趣小组的有6名女生,10名男生;参加物理兴趣小组的有3名女生,5名男生,现采用分层抽样方法从两组中抽取3人.
(1)求抽取的3人中恰有一名女生来自数学兴趣小组的概率;
(2)记X表示抽取3人中男生的人数,求X的分布列和数学期望.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.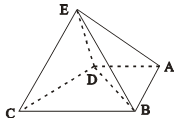
(1)求证:平面DEC⊥平面BDE;
(2)求二面角C—BE—D的余弦值.
已知向量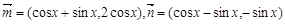 。
。
(1)求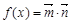 的最小正周期和单调减区间;
的最小正周期和单调减区间;
(2)将函数 的图象向右平移
的图象向右平移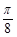 个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将所得图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数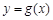 的图象,在△ABC中,角A、B、C的对边分别为
的图象,在△ABC中,角A、B、C的对边分别为 ,若
,若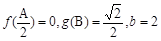 ,求
,求 的值.
的值.
已知数列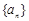 是等差数列,
是等差数列,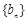 是等比数列,
是等比数列,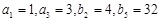 。
。
(1)求数列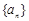 、
、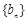 的通项公式;
的通项公式;
(2)设数列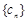 中,
中,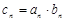 ,求数列
,求数列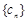 的前n项和Sn.
的前n项和Sn.
如图,菱形ABCD的边长为2,∠BAD=60º, M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).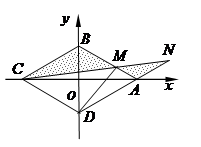
(1)试用t表示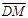 与
与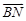 ,并求它们所成角的大小;
,并求它们所成角的大小;
(2)设f(t)=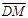 ·
·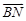 ,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数
,g(t)=at+4-2a(a>0),分别根据以下条件,求出实数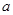 的取值范围:
的取值范围:
①存在t1,t2∈(0,1),使得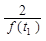 =g(t2);
=g(t2);
②对任意t1∈(0,1),恒存在t2∈(0,1),使得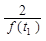 =g(t2).
=g(t2).