在平面直角坐标系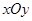 中,已知点
中,已知点 ,
,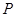 是动点,且
是动点,且 的三边
的三边
所在直线的斜率满足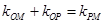 .
.
(Ⅰ)求点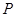 的轨迹
的轨迹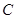 的方程;
的方程;
(Ⅱ)点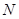 在直线
在直线 上,过
上,过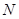 作(Ⅰ)中轨迹
作(Ⅰ)中轨迹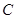 的两切线,切点分别为
的两切线,切点分别为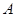 、
、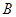 ,若
,若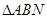
是直角三角形,求点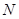 的坐标.
的坐标.
(本小题满分12分)等差数列 中,
中, ,前
,前 项和为
项和为 ,等比数列
,等比数列 各项均为正数,
各项均为正数, ,且
,且 ,
, 的公比
的公比
(1)求 与
与 ;
;
(2)求
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 为菱形,
为菱形, ,
, 为
为 的中点。
的中点。
(1)若 ,求证:平面
,求证:平面 平面
平面 ;
;
(2)点 在线段
在线段 上,
上, ,试确定
,试确定 的值,使
的值,使 平面
平面 ;
;
(本小题满分12分)已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(Ⅰ)若用数组 中的
中的 分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组
分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组 的所有情形,并回答一共有多少种;
的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由。
(本小题满分12分)在 中,
中, 分别是角
分别是角 的对边,若
的对边,若 ,
, 。
。
(1)求角 的大小;
的大小;
(2)若 求
求 面积。
面积。
已知 ,不等式 的解集为 .
(Ⅰ)求
的值;
(Ⅱ)若
恒成立,求
的取值范围.