如图①,正方形AEFG的边长为1,正方形ABCD的边长为3,且点F在AD上.
(1)求 ;
;
(2)把正方形AEFG绕点A按逆时针方向旋转45°得图②,求图②中的 ;
;
(3)把正方形AEFG绕点A旋转一周,在旋转的过程中, 存在最大值与最小值,请直接写出最大值 ,最小值 .
存在最大值与最小值,请直接写出最大值 ,最小值 .
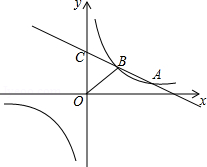
如图,一次函数 与反比例函数 的图象相交于 、 两点,一次函数的图象与 轴相交于点 ,已知点
(1)求反比例函数的解析式;
(2)连接 是坐标原点),若 的面积为3,求该一次函数的解析式.
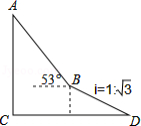
如图,为了测量出楼房 的高度,从距离楼底 处 米的点 (点 与楼底 在同一水平面上)出发,沿斜面坡度为 的斜坡 前进30米到达点 ,在点 处测得楼顶 的仰角为 ,求楼房 的高度(参考数据: , , ,计算结果用根号表示,不取近似值).
某商店购买60件 商品和30件 商品共用了1080元,购买50件 商品和20件 商品共用了880元.
(1) 、 两种商品的单价分别是多少元?
(2)已知该商店购买 商品的件数比购买 商品的件数的2倍少4件,如果需要购买 、 两种商品的总件数不少于32件,且该商店购买的 、 两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
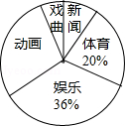
为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
|
节目类型 |
新闻 |
体育 |
动画 |
娱乐 |
戏曲 |
|
人数 |
36 |
90 |
|
|
27 |
根据表、图提供的信息,解决以下问题:
(1)计算出表中 、 的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;
(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
如图, 是线段 的中点, , .求证: .