△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE、PF分别交AB、AC于E、F，给出以下四个结论：
①AE=CF
②△EPF是等腰直角三角形
③EF=AP
④S四边形AEPF=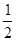
S△ABC
当∠EPF在△ABC内绕P旋转时（点E不与A、B重合）则上述结论始终正确的有（ ）
A．1个 B．2个 C．3个 D．4个
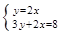
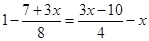
4（2x+3)=9(1-x)-5(x-2)
如图1，在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠AGF=90°，它们的斜边长为
，若∆ABC固定不动，∆AFG绕点A旋转，AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m，CD=n
（1）请在图1中找出两对相似而不全等的三角形，并选取其中一对证明它们相似；
（2）根据图1，求m与n的函数关系式，直接写出自变量n的取值范围；
（3）以∆ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图2). 旋转∆AFG，使得BD=CE，求出D点的坐标，并通过计算验证
；
(4）在旋转过程中,(3)中的等量关系是否始终成立,若成立,请证明,若不成立,请说明理由.