若x1、x2是关于一元二次方程ax2+bx+c（a≠0）的两个根，则方程的两个根x1、x2和系数a、b、c有如下关系：x1+x2=-
，x1•x2=
．把它称为一元二次方程根与系数关系定理．如果设二次函数y=ax2+bx+c（a≠0）的图象与x轴的两个交点为A（x1，0），B（x2，0）．利用根与系数关系定理可以得到A、B两个交点间的距离为：AB=|x1-x2|=
；
参考以上定理和结论，解答下列问题：
设二次函数y=ax2+bx+c（a＞0）的图象与x轴的两个交点A（x1，0），B（x2，0），抛物线的顶点为C，显然△ABC为等腰三角形．
（1）当△ABC为直角三角形时，求b2-4ac的值；
（2）当△ABC为等边三角形时，求b2-4ac的值．
画出数轴，在数轴上表示下列各数，并用“<”连接：
-
， 
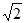，0 ，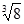
（本题8分）在平面直角坐标系中，已知点P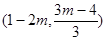
关于
轴的对称点Q在第四象限，且
为整数．
（1）求整数的值；
（2）求△OPQ的面积．
（本题8分）如图，在△ABC，∠BAC＝80º，AD⊥BC于D，AE平分∠DAC，∠B＝60º.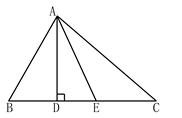
（1）求∠AEC的度数；
（2）想一想，还有其它的求法吗？写出你的思考．
（本题6分） 解不等式：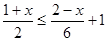
，并把解表示在数轴上．
（本题12分）如图，在△ABC中，已知AB＝AC，∠BAC＝90o，BC＝6cm，，直线CM⊥BC，动点D从点C开始沿射线CB方向以每秒2厘米的速度运动，动点E也同时从点C开始在直线CM上（向上或向下）以每秒1厘米的速度运动，连结AD、AE，设运动时间为t秒．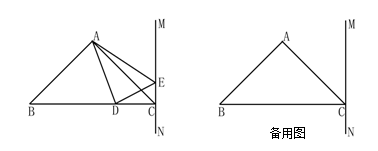
（1）求AB的长；
（2）当t为多少时，△ABD的面积为6cm2？
（3）当t为多少时，△ABD≌△ACE，并简要说明理由（可在备用图中画出具体图形）．