某同学用如图所示的实验装置验证牛顿第二定律，小车上固定有宽度为d的遮光条，他将光电门固定在长木板上的B点，用重物通过细线与固定在小车前端的力传感器相连（力传感器可测出细线的拉力大小）。每次小车都从同一位置A由静止释放，改变砝码个数并测出小车的质量m（含砝码、传感器与遮光条），测出对应拉力传感器的示数F和对应遮光条通过光电门的时间Δt。
试回答下列问题：
（1）若A、B间的距离为L，则计算小车加速度的表达式为a= 。
（2）根据测得的实验数据，以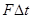
为纵轴，以 为横轴，若得到一条过原点的直线，则可验证牛顿第二定律。
（3）关于本实验，某同学提出如下观点，其中不正确的是（ ）
A．L越大，实验误差越小
B．牵引小车的细绳应与木板平行
C．应平衡小车受到的摩擦力
D．重物的质量应远小于小车的质量
在“描述小灯泡的伏安特性曲线”实验中，需要用伏安法测定小灯泡两端的电压和通过小灯泡的电流，除开关、导线外，还有如下器材：
A．小灯泡“6V 3W ”
B．直流电源6 ~ 8V
C．电流表（量程3A，内阻0．2 Ω ）
D．电流表（量程0．6A，内阻 1 Ω ）
E．电压表（量程6 V ，内阻20 kΩ ）
F．电压表（量程20V ，内阻60 kΩ ）
G．滑动变阻器（0 ~ 20 Ω、2 A）
H．滑动变阻器（1 kΩ、0．5 A）
（1）把实验所用到的器材按字母的先后顺序填入空中：
（2）在下面的虚线框内画出最合理的实验原理图．
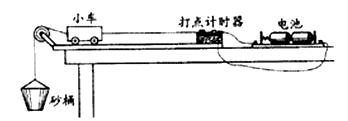
①如图所示为某同学所安装的“验证牛顿第二定律”的实验装置，若在图示状态下开始做实验，请从该同学的装置和操作中指出存在的问题或错误__________
______________________________________________________________________________________________________________________________________________
②下图是①中更正后实验打出的一条纸带，已知打点计时器的打点周期是0．02s，求出小车运动加速度的大小为m/s2，（计算结果保留2位有效数字）
在液体中下落的物体最终会达到一个恒定的速度，称之为收尾速度。一个半径为r的球体在液体中下落的收尾速度为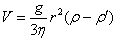
，其中
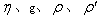
分别为液体的粘滞系数（与液体种类相关的常数）、重力加速度（本题中为已知量）、球体的密度、液体的密度。某同学为了测定某已知密度的液体的粘滞系数，选定了下列器材：一只1000mL的量筒；一块秒表；一把刻度尺；直径不同的铝球若干个（最大直径约10.00mm）。
⑴请列出该同学漏选的器材：。
⑵实验时，该同学首先将直径约10.00mm的铝球重复从装满被测液体的量筒液面上自由落下测定它通过量筒刻线750mL到500mL和450mL到200mL的两段时间，列表如下：
| 距离L（mL） |
时间t(s) |
平均时间t/(s) |
| 750～500 |
1.74 1.72 1.72 |
1.73 |
| 450～200 |
1.73 1.72 1.73 |
1.73 |
由以上测量数据得到的结论是。
⑶若测出了不同半径的铝球的收尾速度，要求出液体的粘滞系数，对以上数据应如何处理？
完成以下两题
（1）如图为某同学在做匀变速直线运动实验中获得的一条纸带。
①已知打点计时器电源频率为50Hz，则纸带上打相邻两点的时间间隔为_________。
②ABCD是纸带上四个计数点，每两个相邻计数点间有四个
点没有画出。从图中读出A、B两点间距s=__________；C点对应的速度是________(计算结果保留三位有效数字)。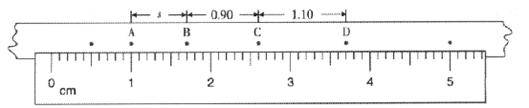
（2）如图为验证机械能守恒定律的实验装置示意图。现有的器材为：带铁夹的铁架台、电磁打点计时器、纸带、带铁夹的重锤、天平。回答下列问题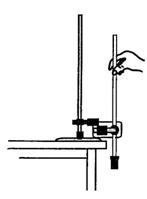
①为完成此实验，除了所给的器材，还需要的器材有______
A、米尺B、秒表C、0～12V的直流电源D、0～12V的交流电源
②实验中误差产生的原因有。(写出两个原因)
现有一满偏电流为500μA，内阻为1.2×103Ω的电流表，某同学想把它改装成中值电阻为600Ω的欧姆表，（中值电阻：电阻调零后，当测量待测电阻时，电流表指针指在表盘中央时所对应的阻值）实验室提供如下器材：
| A．一节干电池（标准电动势为1.5V） | B．电阻箱R1（最大阻值99.99Ω） |
| C．电阻箱R2（最大阻值999.9Ω） | D．滑动变阻器R3（0—100Ω） |
E、滑动变阻器R4（0—1KΩ ） F、导线若干及两个接线柱
（1）为完成实验，上述器材中应选择_______、_______、_______、_______（填器材前面的字母代号）
（2）在方框中画出改装电路图。
（3）用改装后的欧姆表测一待测电阻，读出电流表的读数为200μA，则待测电阻阻值为_____________Ω。