已知直线y=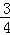
x﹣3与x轴交于点A，与y轴交于点C，抛物线y=﹣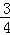x2+mx+n经过点A和点C．
（1）求此抛物线的解析式；
（2）在直线CA上方的抛物线上是否存在点D，使得△ACD的面积最大？若存在，求出点D的坐标；若不存在，说明理由．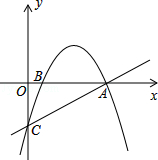
如图，在平面直角坐标系xOy中，矩形ABCD的边AD=3，A（
，0），B（2，0），
直线y=kx+b经过B，D两点．
（1）求直线y=kx+b的解析式；
（2）将直线y=kx+b平移，若它与矩形有公共点，直接写出b的取值范围．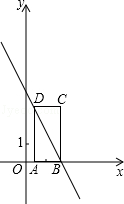
列方程解应用题：
A地区2011年公民出境旅游总人数约600万人，2013年公民出境旅游总人数约864万人，若2012年、2013年公民出境旅游总人数逐年递增，请解答下列问题：
（1）求2012、2013这两年A地区公民出境旅游总人数的年平均增长率；
（2）如果2014年仍保持相同的年平均增长率，请你预测2014年A地区公民出境旅游总人数约多少万人？
摆棋子游戏：现有4个棋子A，B，C，D，要求棋子A必须摆放在第一位置，其余3个随机摆放在第二、三、四的位置．
（1）请你列举出所有摆放的可能情况；
（2）求出棋子C摆放在偶数位置的概率．
如图，直线y=kx﹣2与x轴交于点A（1，0），与y轴交于点B，若直线AB上的点C在第一象限，且S△BOC=3，求点C的坐标．
