某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t后甲、乙两遥控车与B处的距离分别为 ,
, ,则
,则 ,
, 与t的函数关系如图,试根据图象解决下列问题:
与t的函数关系如图,试根据图象解决下列问题:
(1)填空:乙的速度 = 米/分;
= 米/分;
(2)写出 与t的函数关系式;
与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
魔术师为大家表演魔术. 他请观众想一个数,然后将这个数按以下步骤操作:
魔术师立刻说出观众想的那个数.
(1)如果小明想的数是 ,那么他告诉魔术师的结果应该是;
,那么他告诉魔术师的结果应该是;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,请你说出其中的奥妙.
检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发, 到收工时,行走记录为(单位:千米):
+8、-9、+4、+7、-2、-10、+18、-3、+7、+5
回答下列问题:
(1)收工时检修组在A地的哪边?距A地多少千米?
(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?
先化简,再求值 ,其中
,其中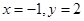 .
.
一个多项式,当减去 时,某学生因把“减去”误认为“加上”,得到结果
时,某学生因把“减去”误认为“加上”,得到结果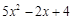 ,原来这个多项式应是什么?
,原来这个多项式应是什么?
