如图,在梯形ABCD中,AB∥CD,∠BAD=90°,以AD为直径的半圆O与BC相切.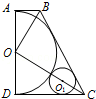
(1)求证:OB⊥OC;
(2)若AD=12,∠BCD=60°,⊙O1与半⊙O外切,并与BC、CD相切,求⊙O1的面积.
(1)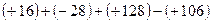
(2)
出租车收费标准因地而异. A市为:行程不超过3千米收起步价12元,超过3千米后每千米增收1.2元;B市为:行程不超过3千米收起步价10元,超过3千米后每千米增收1.4元.设在A、B两市乘坐出租车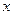
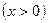 千米.
千米.
(1)若小明分别在A、B两市乘坐出租车行驶了相同的行程8千米,试分别计算出两次乘车的费用;
(2)在A、B两市乘坐出租车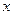 千米
千米 的费用相差多少元,试用含
的费用相差多少元,试用含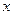 的代数式表示
的代数式表示
某校为了研究中学生是否应带手机到校园,现委托学生会对同学带手机到校园的主要用途进行调查统计,经统计整理,绘制成不完整的扇形统计图与条形统计图如下,请回答如下问题:

(1)本次共调查了多少人?
(2)请计算出学生带手机主要用于上网的人数;
(3)分别把条形统计图和扇形统计图补充完整(标出角度及百分比)
判断下列各式是否成立。你认为成立的请在( )内打“√”号,不成立的打“×”号。
① ()②
()② ()
()
③ ()④
()④ ()
()
你判断完以后,你肯定发现了某个规律,请你用含 的式子将规律表示出来。
的式子将规律表示出来。
请你观察思考下列计算过程:
∵ ,∴
,∴ ;
;
同样:∵ ,∴
,∴ ;……………………………
;……………………………
由此猜想 。
。