已知 求
求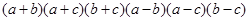 的值。
的值。
如图,在平面直角坐标系中,四边形ABCD为矩形,BC平行于x轴,AB=6,点A的横坐标为2,反比例函数y= 的图像经过点A、C.
的图像经过点A、C.
(1)求点A的坐标;
(2)求经过点A、C所在直线的函数关系式.
(3)请直接写出AD长.
如图,在□ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F,连接BD.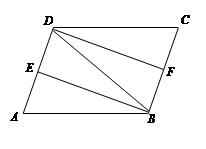
(1)求证:△ABE≌△CDF;
(2)若AB=DB,求证:四边形DFBE是矩形.
河西某滨江主题公园有A、B两个出口,进去游玩的甲、乙、丙三人各自随机选择一个出口离开,求他们三人选择同一个出口离开的概率.
3月的南京,“春如四季”.如图所示为3月22日至27日间,我市每日最高气温与最低气温的变化情况.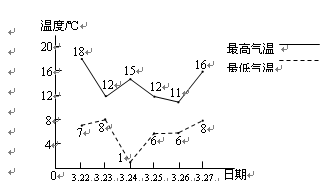
(1)最低气温的中位数是℃;3月24日的温差是℃;
(2)分别求出3月22日至27日间的最高气温与最低气温的平均数;
(3)数据更稳定的是最高气温还是最低气温?说说你的理由.
先化简,再求值:( -
- )÷
)÷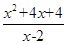 ,其中x是方程x2-2x=0的根.
,其中x是方程x2-2x=0的根.