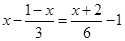如图, 已知 为直线
为直线 上一点,过点
上一点,过点 向直线
向直线 上方引三条射线
上方引三条射线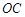 、
、 、
、 , 且
, 且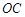 平分
平分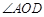 ,
,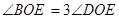 ,
,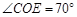 ,求
,求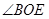 的度数.
的度数.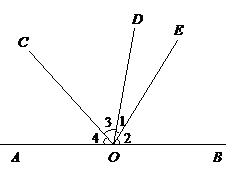
如下的两幅不完整的统计图反映了重庆一中校男子篮球队的年龄分布情况: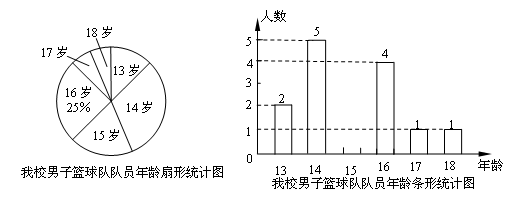
请根据图中提供的信息,解答下列问题:
(1)重庆一中校男子篮球队队员有多少人?
(2)将条形统计图补充完整;
(3)在扇形统计图中,求出“15岁”部分所对应的圆心角的度数;
(4)重庆一中校男子篮球队队员的平均年龄是多少?
列方程解应用题:
小明和小东两人练习跑步,都从甲地出发跑到乙地,小明每分钟跑250米,小东每分钟跑200米,小明让小东先出发3分钟之后再出发,结果两人同时到达乙地,求甲、乙两地之间的路程是多少米?
先化简,再求值:
若 ,求代数式
,求代数式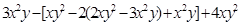 的值.
的值.
解方程: