在一场2015亚洲杯赛B组第二轮比赛中，中国队凭借吴曦和孙可在下半场
的两个进球，提前一轮小组出线。如图，足球场上守门员在
处开出一高球，球从离地面1米的
处飞出
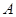（在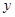
轴上），运动员孙可在距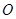点6米的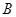
处发现球在自己头的正上方达到最高点
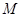，距地面约4米
高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高
度减少到原来最大高度的一半．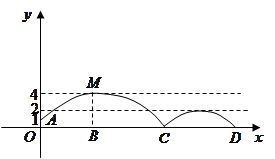
(1)、求足球开始飞出到第一次落地时，该抛物线的函数表达式．
(2)、足球第一次落地点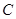
距守门员多少米？（取
）
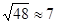(3)、孙可要抢到足球第二个落地点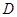
，他应从第一次落地点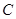再向前跑多少米？（取
）
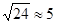如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在格点上，在建立平面直角坐标系后，点A的坐标为（－5，1），点B的坐标为（－3，3），点C的坐标为（－3，1）。
（1）将Rt△ABC沿x轴正方向平移7个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1的图形;
（2）Rt△ABC关于点D（－1，0）对称的图形是Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形,并写出A2、B2、C2点的坐标。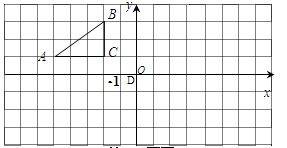
先化简，再求值（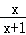
﹣1）÷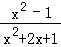
，其中x=2sin60°+1．
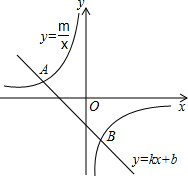
已知：如图，正比例函数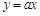
的图象与反比例函数
的图象交于点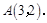
（1）试确定上述正比例函数和反比例函数的表达式；
（2）根据图象回答，在第一象限内，当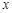
取何值时，反比例函数的值大于正比例函数的值？
（3）M(m,n)是反比例函数图像上的一动点,其中0<m<3,过M作直线MB‖x轴交y轴于点B。过点A作直线AC∥y轴交于点C，交直线MB于点D，当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由；
（4）探索：x轴上是否存在点P,使ΔOAP是等腰三角形？若存在，求出点P的坐标，若不存在，请说明理由。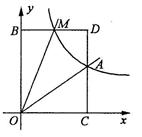
在购买某场足球赛门票时，设购买门票数为x（张），总费用为y（元）．现有两种购买方案：
方案一：若单位赞助广告费10000元，则该单位所购门票的价格为每张60元；
（总费用＝广告赞助费+门票费）
方案二：购买门票方式如图所示．
解答下列问题：
（1）方案一中，y与x的函数关系式为；
方案二中，当0≤x≤100时，y与x的函数关系式为，
当x＞100时，y与x的函数关系式为；
（2）如果购买本场足球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；
（3）甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张，花去总费用计58000元，求甲、乙两单位各购买门票多少张．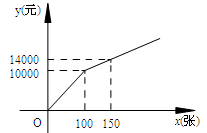
如图，已知A（－4，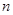
）、B（2，－4）是一次函数
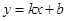的图象和反比例函数
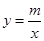的图象的两个交点。
（1）求反比例函数和一次函数的解析式；
（2）求直线AB和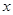
轴的交点C的坐标及△AOB的面积；
（3）求方程
的解（请直接写出答案）；
（4）求不等式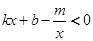
的解集（请直接写出答案）。