如图，在竖直向下的磁感应强度为B的匀强磁场中，两根足够长的平行光滑金属轨道MN、PQ固定在水平面内，相距为L。一质量为m的导体棒ab垂直于MN、PQ放在轨道上，与轨道接触良好。轨道和导体棒的电阻均不计。
（1）如图1，若轨道左端接一电动势为E、内阻为r的电源和一阻值未知的电阻。闭合开关S，导体棒从静止开始运动，经过一段时间后，导体棒达到稳定最大速度vm，求此时电源的输出功率。
（2）如图2，若轨道左端接一电容器，电容器的电容为C，导体棒在水平恒定拉力的作用下从静止(t=0)开始向右运动。已知tc时刻电容器两极板间的电势差为Uc。求导体棒运动过程中受到的水平拉力大小。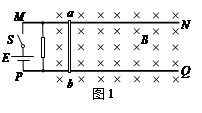
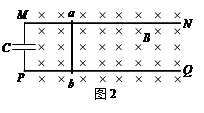
在如图所示的匀强电场中，有A、B两点，且A、B两点间的距离为x="0.20" m，已知AB连线与电场线夹角为
=60°，今把一电荷量
C的检验电荷放入该匀强电场中，其受到的电场力的大小为
N，方向水平向左。求：
（1）电场强度E的大小和方向；
（2）若把该检验电荷从A点移到B点，电势能变化了多少；
（3）若A点为零电势点，B点电势为多少。
如图所示，电阻R1=6Ω，R2=4Ω，电源电动势为20V，闭合电建后，若电路消耗的总功率为40W，电源输出功率为37.6W，求：电源的内阻r和R3的阻值分别为多大。
如图所示，绷紧的传送带，始终以v=2m/s的速度匀速斜向上运行，传送带与水平方向间的夹角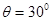
．现把质量m=10kg的工件轻轻地放在传送带底端P处，由传送带传送至顶端Q处．已知PQ之间的距离为4m，工件与传送带间的动摩擦因数为
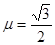，取g=10m/s2．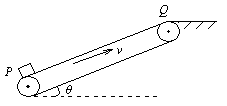
（1）通过计算说明工件在传送带上做什么运动；
（2）求工件从P点运动到Q点所用的时间．
静止在水平面上的A、B两个物体通过一根拉直的轻绳相连，如图所示，轻绳长L=1m，承受的最大拉力为8N，A的质量m1=2kg，B的质量m2=8kg，A、B与水平面间的动摩擦因数μ=0.2，现用一逐渐增大的水平力F作用在B上，使A、B向右运动，当F增大到某一值时，轻绳刚好被拉断．(A、B可当做质点，g=10m/s2)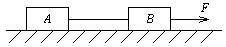
（1）求绳刚被拉断时F的大小；
（2）若绳刚被拉断时，A、B两物体的速度为2m/s，保持此时的F大小不变，则当A物体速度恰减至零时，A、B两物体间的距离为多少?
A物体做速度为1m/s的匀速直线运动，A出发后的6s末，B物体从同一地点由静止出发做匀加速直线运动，加速度为2m/s2，且A、B运动方向相同，问：
（1）B出发后经过多长时间追上A；
（2）A、B相遇前，它们之间的最大距离为多少？