(本题12分)如图1,在长方形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿
A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象: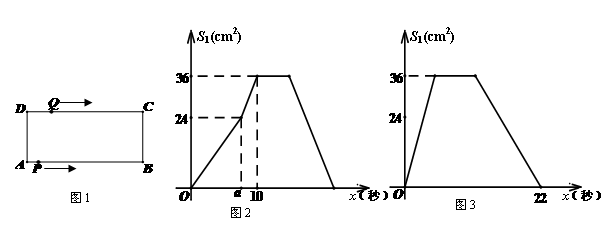
(1)请直接写出a= 、b= 、c= ;
(2)设点P离开点A的运动路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后y1、y2与出发后的运动时间x(秒)的函数表达式,并求出P与Q相遇时x的值.
如图,某小区有一块长为24米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为72米2,两块绿地之间及周边留有宽度相等的人行通道,求人行道的宽度.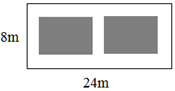
先化简,再求值: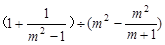 ,其中
,其中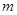 是方程
是方程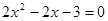 的根.
的根.
解下列方程:
(1)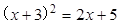 ;
;
(2)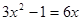 (用配方法).
(用配方法).
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠EAC=∠B.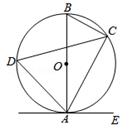
(1)求证:直线AE是⊙O的切线;
(2)若∠D=60°,AB=6时,求劣弧AC的长(结果保留π).
已知,如图,直线MN交⊙O于A,B两点,AC是⊙O的直径,DE切⊙O于点D,且DE⊥MN于点E.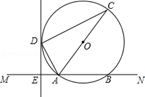
(1)求证:AD平分∠CAM.
(2)若DE=6,AE=3,求⊙O的半径.