（本题10分）如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，AB=25，顶点C在y轴的负半轴上，tan∠ACO=
，点P在线段OC上，且PO、PC的长（PO<PC）是关于x的方程x2-12x+32=O的两根．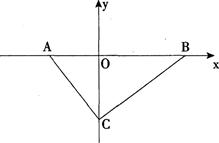
（1） 求P点坐标求
（2） 求AC、BC的长；
（3）在x轴上是否存在点Q，使以点A、C、P、Q为顶点的四边形是梯形?若存在，请直接写出直线PQ的解析式；若不存在，请说明理由．
如图，已知线段a及∠O，只用直尺和圆规，求做△ABC，使BC=a，∠B=∠O，∠C=2∠B（在指定作图区域作图，保留作图痕迹，不写作法）
如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上，按要求画一个三角形，使它的顶点在方格的顶点上。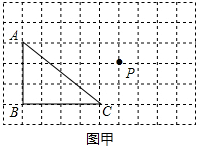
（1）将△ABC平移，使点P落在平移后的三角形内部，在图甲中画出示意图；
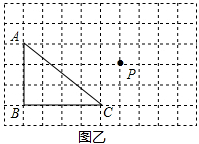
（2）以点C为旋转中心，将△ABC旋转，使点P落在旋转后的三角形内部，在图乙中画出示意图。
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB，于点E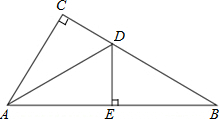
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长。
化简：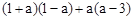
计算：
；