如图,△ 为一锐角三角形,
为一锐角三角形,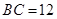 ,
, 边上的高
边上的高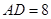 .点
.点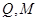 在边
在边 上,
上,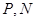 分别在边
分别在边 上,且
上,且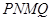 为矩形.
为矩形.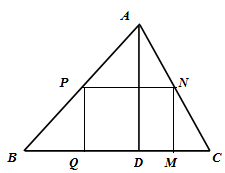
(1)设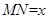 ,用
,用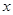 表示
表示 的长度;
的长度;
(2)当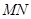 长度为多少时,矩形
长度为多少时,矩形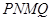 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
(3)当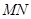 长度为多少时,△
长度为多少时,△ 的面积等于△
的面积等于△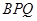 与△
与△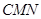 之和?
之和?
2015年5月,某校组织了以“德润书香”为主题的电子小报制作比赛,评分结果只有60,70,80,90,100五种,现从中随机抽取部分作品,对其份数和成绩进行整理,制成如下两幅不完整的统计图:
根据以上信息,解答下列问题:
(1)求本次抽取了多少份作品,并补全两幅统计图;
(2)已知该校收到参赛作品共900份,比赛成绩达到90分以上(含90分)的为优秀作品,据此估计该校参赛作品中,优秀作品有多少份?
先化简,再求值:(1+ )÷
)÷ ,其中:x=3
,其中:x=3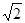 ﹣3.
﹣3.
如图,抛物线 交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).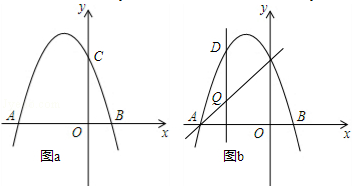
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且 ,求点P的坐标;
,求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.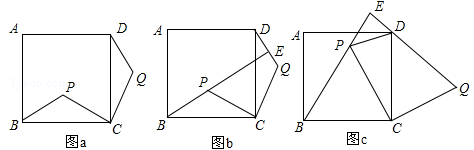
(1)如图a,求证:△BCP≌△DCQ;
(2)如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
为了丰富学生的体育生活,学校准备购进一些篮球和足球,已知用900元购买篮球的个数比购买足球的个数少1个,足球的单价为篮球单价的0.9倍.
(1)求篮球、足球的单价分别为多少元?
(2)如果计划用5000元购买篮球、足球共52个,那么至少要购买多少个足球?