（本小题满分12分）编号分别为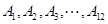
的
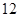名篮球运动员在某次篮球比赛中的得分记录如下:
（1）完成如下的频率分布表:
| 得分区间 |
频数 |
频率 |
 |
3 |
 |
 |
|
|
 |
|
|
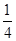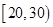| 合计 |
|
 |
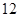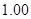（2）从得分在区间
内的运动员中随机抽取
人 ， 求这人得分之和大于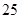
的概率.
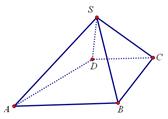
如图，四棱锥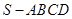
中，
∥
,
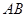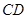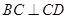，侧面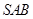
为等边三角形
（1）证明：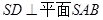
（2）求AB与平面SBC所成角的正弦值
已知：以点C(t,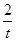
)(t∈R,t≠0)为圆心的圆与
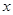轴交于点O,A，与y轴交于点O,B，其中O为原点
（1）求证：△OAB的面积为定值；
（2）设直线y=–2x+4与圆C交于点M,N，若OM=ON，求圆C的方程
已知圆C：
=0
（1）已知不过原点的直线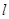
与圆C相切，且在
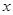轴，
轴上的截距相等，求直线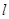的方程；
（2）求经过原点且被圆C截得的线段长为2的直线方程
如图，在正方体
中，
（1）求证：
;
（2）求直线
与直线BD所成的角
某工厂为了制造一个实心工件，先画出了这个工件的三视图（如图），其中正视图与侧视图为两个全等的等腰三角形，俯视图为一个圆，三视图尺寸如图所示（单位cm）；
（1）求出这个工件的体积；
（2）工件做好后，要给表面喷漆，已知喷漆费用是每平方厘米1元，现要制作10个这样的工件，请计算喷漆总费用（精确到整数部分）.