在平面直角坐标系中，抛物线
与x轴的两个交点分别为A（-3，0），B（1，0），过顶点C作CH⊥x轴于点H．
（1）a= ，b= ，顶点C的坐标为 ．
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由．
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标．
如图，已知△ABC中，∠B=∠C，AB=AC=10厘米，BC=8厘米，点D为AB的中点．
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？
如图，正方形ABCD和正方形BEFG平放在一起．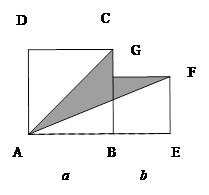
（1）若两正方形的面积分别是9和4，直接写出边AE的长为_________．
（2）①设正方形ABCD的边长为a,正方形BEFG的边长为b,求图中阴影部分的面积（用含a和b的代数式表示）
②在①的条件下，如果a+b=20,ab=96，求阴影部分的面积．
如图，在△ABC中，∠ACB=90°,AC=BC，直线l经过顶点C，过A，B两点分别作l的垂线AE，BF，垂足为E，F．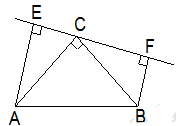
（1）求证：△ACE≌△CBF
（2）当直线l不与底边AB相交时，试探索EF、AE、BF三条线段的大小关系，并说明理由．
如图，某校有一块长为（3a＋b）米，宽为（2a+b）米的长方形地块，学校计划将阴影部分进行绿化，中间将修建一座雕像．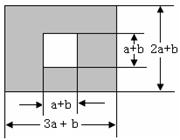
（1）用含a、b的代数式表示绿化面积；
（2）求出当a=3米,b=2米时的绿化面积．
如图，已知AB=DC，∠ABC=∠DCB．求证:△ABC≌△DCB