(1)如图(1)∠AOB和∠COD都是直角,请你指出∠AOD和∠BOC之间的数量关系;
(2)当∠COD绕点O旋转到如图(2)所示的位置时,上述结论还成立吗?请说明理由.
(3)如图(3),当∠AOB=∠COD=β(0°<β<90°)时,请你直接写出∠AOD和∠BOC之间的数量关系(不用说明理由).

已知:如图,在矩形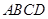 中,
中,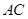 是对角线.点
是对角线.点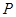 为矩形外一点且满足
为矩形外一点且满足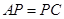 ,
,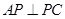 .
.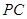 交
交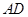 于点
于点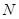 ,连接
,连接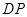 ,过点
,过点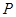 作
作 交
交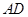 于
于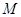 .
.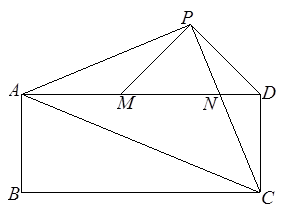
(1)若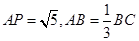 ,求矩形
,求矩形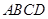 的面积;
的面积;
(2)若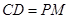 ,求证:
,求证: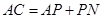 .
.
为配合学校开展的“书香校园读书日”活动,我校初二某班的社会实践活动小组就该班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图: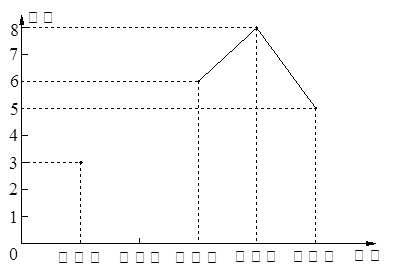
(1)已知这五周“读书之星”人数的众数为8人,求该班这五周“读书之星”人数的平均数;
(2)将折线统计图补充完整;
(3)若第五周的“读书之星”同学中,同学A和B一直坚持得比较好,现在该社会实践活动小组将从第五周的“读书之星”中,随机抽出两位同学谈谈他们的收获,请你用列表或画树状图的方法,求出所选两位同学恰好是同学A和B的概率.
如图,在平面直角坐标系中,点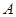 是反比例函数
是反比例函数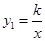
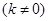 图象上一点,
图象上一点,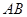 ⊥
⊥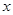 轴于
轴于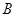 点,一次函数
点,一次函数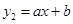
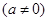 的图象交
的图象交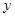 轴于
轴于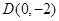 ,交
,交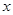 轴于
轴于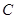 点,并与反比例函数的图象交于
点,并与反比例函数的图象交于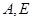 两点,连接
两点,连接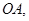 若△
若△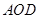 的面积为4,且
的面积为4,且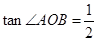 .
.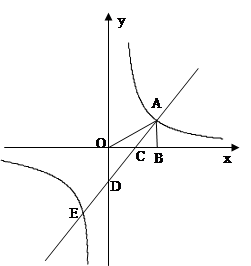
(1) 分别求出该反比例函数和一次函数的解析式;
(2) 求△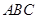 的面积.
的面积.
先化简,再求值: ,其中x是不等式组
,其中x是不等式组 的整数解.
的整数解.
已知在△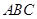 中,∠
中,∠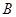 =30°,
=30°,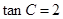 ,
,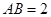 ,求△
,求△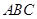 的周长.
的周长.
(结果保留根号)