(本小题满分14分)
如图,2015年春节,摄影爱好者 在某公园
在某公园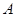 处,发现正前方
处,发现正前方 处有一立柱,测得立柱顶端
处有一立柱,测得立柱顶端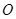 的仰角和立柱底部
的仰角和立柱底部 的俯角均为
的俯角均为 ,已知
,已知 的身高约为
的身高约为 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按 米处理)
米处理)
(1) 求摄影者到立柱的水平距离和立柱的高度;
(2) 立柱的顶端有一长2米的彩杆 绕中点
绕中点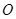 在
在 与立柱所在的平面内旋转.摄影者有一视角范围为
与立柱所在的平面内旋转.摄影者有一视角范围为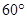 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
已知某商品生产成本 与产量
与产量 的函数关系式为
的函数关系式为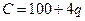
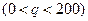 ,价格
,价格 与产量
与产量 的函数关系式为
的函数关系式为 ,求产量
,求产量 为何值时,利润
为何值时,利润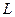 最大。
最大。
已知复数 ,当实数m取什么值时,复数z是(1) 零 (2)虚数 (3)纯虚数
,当实数m取什么值时,复数z是(1) 零 (2)虚数 (3)纯虚数
已知 是函数
是函数 的一个极值点,其
的一个极值点,其 ,
,
(1)求 与
与 的关系式;
的关系式;
(2)求 的单调区间;
的单调区间;
(3)当 时,函数
时,函数 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3 ,求
,求 取值范围
取值范围
己知下列三个方程: x2+4ax-4a+3="0," x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根,求实数a的取值范围.
(本题满分12分)如图,正四棱柱ABCD—A1B1C1D1中,底面边长为 ,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
,侧棱长为4,E、F分别是棱AB,BC的中点,EF与BD相交于G.
(1)求证:B1EF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离d;
(3)求三棱锥B1—EFD1的体积V.