某省为了研究雾霾天气的治理,一课题组对省内24个城市进行了空气质量的调查,按地域特点把这些城市分成了甲、乙、丙三组.已知三组城市的个数分别为4,8,12,课题组用分层抽样的方法从中抽取6个城市进行空气质量的调查.
(I)求每组中抽取的城市的个数;
(II)从已抽取的6个城市中任抽两个城市,求两个城市不来自同一组的概率.
已知等比数列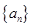 的公比
的公比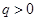 ,且
,且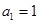 ,
, .
.
(Ⅰ)求公比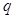 和
和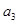 的值;
的值;
(Ⅱ)若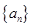 的前
的前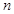 项和为
项和为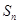 ,求证
,求证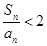 .
.
已知x为实数,用表示不超过x的最大整数,例如 对于函数f(x),若存在
对于函数f(x),若存在 ,使得
,使得 ,则称函数
,则称函数 函数.
函数.
(Ⅰ)判断函数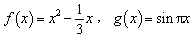 是否是
是否是 函数;(只需写出结论)
函数;(只需写出结论)
(Ⅱ)设函数f(x)是定义R在上的周期函数,其最小正周期为T,若f(x)不是 函数,求T的最小值.
函数,求T的最小值.
(Ⅲ)若函数 是
是 函数,求a的取值范围.
函数,求a的取值范围.
已知由整数组成的数列 各项均不为0,其前n项和为 ,且
各项均不为0,其前n项和为 ,且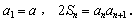
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的通项公式;
的通项公式;
(Ⅲ)若 时,
时,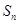 取得最小值,求a的值.
取得最小值,求a的值.
已知函数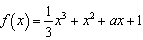 ,曲线
,曲线 在点(0,1)处的切线为l
在点(0,1)处的切线为l
(Ⅰ)若直线l的斜率为-3,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数是 区间[-2,a]上的单调函数,求a的取值范围.
区间[-2,a]上的单调函数,求a的取值范围.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,

(Ⅰ)求BD的长;
(Ⅱ)求证: